Расчет и построение графиков обслуживания

Горной машины

В расчетной работе рассмотрен вероятностный способ организации профилактических работ, основанный на анализе статистической информации о надежности. Целью расчетов является определение оптимальных сроков службы элементов горных машин, при которых достигается минимум затрат на проведение плановых и аварийных ремонтов, построение стратегии обслуживания горного оборудования и определение необходимого количества запасных частей.

Порядок выполнения работы:

1. Определение параметров законов распределения случайных наработок узлов и деталей машины.

2. Выбор наиболее вероятных законов распределения наработки каждого узла машины.

3. Расчет оптимального периода замены каждого узла машины, определение сроков и видов ремонтов, выбор количества запасных частей.

4. Построение графиков ремонтов.

Определение параметров распределения наработок 1-го узла выполнено путем статистической обработки накопленных данных на ЭВМ. Получены следующие результаты:

Нормальный закон	T_ср = 1780	s = 650
Логарифмически-нормальный закон	А = 4,8124	s_л = 0,236
Закон Вейбулла	А = 1884	В = 5,006
Гамма-распределения	l = 0,00252	m = 10,41

Для построения диаграммы и опытной кривой распределения наработок 1-го узла определяем длину интервала

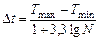, (6.1)

где T_maxи T_min– соответственно максимальная и минимальная наработка 1-го узла машины по статистическим данным,

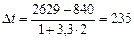На рис. 6.2 представлены результаты построения диаграммы и кривой распределения наработок для 1-го узла.

Наиболее вероятный закон распределения наработок каждого узла выбирается с помощью критерия согласия Пирсона c²(табл. 6.1):

Рис.6.2. Диаграмма и опытная кривая распределения

наработок 1-го узла

Таблица 6.1

Коэффициенты критерия согласия Пирсона c²

Законы распределения	первый узел	второй узел	третий узел	четвертый узел	пятый узел
Нормальный	13,45	14,90	23,46	18,86	13,58
Логарифмически-нормальный	28,40	26,33	16,32	17,28	33,80
Вейбулла	4,64	4,47	16,86	20,16	5,71
Гамма	10,08	34,056	10,39	4,23	22,64

По значению критерия согласия выбраны законы распределения: первый, второй, пятый узлы – закон Вейбулла; третий, четвертый узлы – гамма-распределения.

В качестве критерия для расчета оптимальных сроков замен (табл. 6.2.) используем отношение затрат на замену узла к длительности межремонтного периода S_уд и коэффициент стоимости узла Е, значение которого приведено в исходных данных. В результате расчетов на ЭВМ получены значения оптимальных сроков замены Т_опт, средние значения наработок Т_ср, вероятности достижения оптимальных сроков замены wи удельные стоимости замен S_уд:

Таблица 6.2

<33 34 353637 38 39 >

Дата добавления: 2020-05-20; просмотров: 449;