Примеры расчета оптимального периода профилактических ремонтов

Пример 1. Хронометражные наблюдения за работой комплекса для возведения набрызг-бетонной крепи дали следующие результаты:

-среднее время безотказной работы узла для приготовления сухой смеси Т_ср = 50 ч;

-время технологического перерыва р = 6 ч;

-время работы узла между технологическими перерывами
r = 10 ч;

-средняя длительность аварийного ремонта а = 10 ч;

-средняя длительность полного профилактического ремонта
S = 8 ч.

Так как плотность потока отказов растет с течением времени, то в качестве закона распределения времени безотказной работы можно принять закон Вейбулла, для которого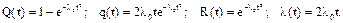

Найдем l₀ для закона Вейбулла из условия 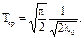Отсюда l₀ = 0,0003 1/ч. Так как 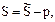то S = 2 ч. Таким образом:

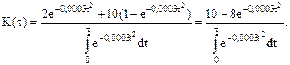
Интеграл вычисляем по формуле

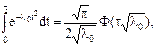
где 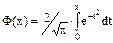-функция Лапласа.

Для расчета оптимального числа полных рабочих периодов между профилактиками m* и минимума коэффициентов простоя K(t) можно использовать аналитический пакет MAPLE.

Исходные данные: А = 10,0; Т = 50,0;

R = 10,0; d = 2,0.

Результаты: Количество итераций J = 3.

Начальное значение для поиска «М» М₁ = 1.

Число полных рабочих периодов М = 3.

Коэффициент простоя SK₁ = 0,1452.

Следует отметить, что без профилактики K(t) = 0,2.

Пример 2. Рассмотрим работу горнопроходческого комплекса, состоящего из бурового агрегата А и погрузочной машины Б. Работа этих механизмов осуществляется последовательно, и любая неисправность агрегата при нахождении его в забое должна быть устранена немедленно, прежде чем будет произведен взрыв и в забой будет введена погрузочная машина.

Исходные данные:

- среднее время безотказной работы бурового агрегата Т_ср = 35 ч;

- средняя длительность плановой профилактики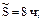

- время технологического перерыва p = 6 ч; средняя длительность аварийного ремонта a = 9 ч;

- время работы между технологическими перерывами r = 5 ч;

- время работы до первого аварийного ремонта r¢ = 3 ч.

Выбрав закон Вейбулла 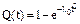в качестве закона распределения времени безотказной работы, аналогично примеру 1 получим l₀ = 0,0006, а = 9 ч, S = 2 ч, Т = 35 ч, r = 5 ч, r¢ = 3 ч.

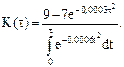
Используем аналитический пакет MAPLE.

Исходные данные: А = 9,0; Т = 35,0; R = 5,0; S = 2,0.

Результаты:Количество итераций J = 4.

Начальное значение для поиска «М» М₁ = 1.

Число полных рабочих периодов М = 4.

Коэффициент простоя SK₁ = 0,1960.

Для определения оптимального числа m* полных периодов между аварийным и профилактическим ремонтами вычисляем для ряда значений 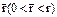величины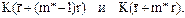

Принимая 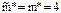, получим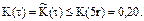

Пример 3. Погрузочно-транспортный комплекс состоит из погрузочной машины А и транспортера с бункером-накопителем Б, откуда грунт поступает в транспортные средства. В этом случае при отказе погрузочной машины уборка грунта часть времени (или все время), необходимого для аварийного ремонта, не прекращается, так как находящийся на транспортере и в бункере грунт продолжает поступать в транспортные сосуды.

Пусть для погрузочной машины Т_ср = 40 ч; 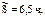a = 7,5 ч; р = 6 ч; r = 3 ч.

Тогда l₀ = 0,0005; q = р/r = 2; S = 0,5 ч; a > qr.

Для расчета оптимального периода m* используем аналитический пакет MAPLE.

Исходные данные: А = 7,5; Т = 40,0; R = 3,0; S = 0,5;

p = 6,0.

Результаты:Количество итераций J = 6.

Начальное значение для поиска «М» М₁ = 1.

Число полных рабочих периодов М = 6.

Коэффициент простоя SK₁ = 0,0756.

Пример 4. Рассмотрим работу бетоно-смесительного узла, состоящего из устройств для подачи материалов (заполнителей, цемента и воды) А₁ через расходные бункеры в бетоносмеситель А₂, из которого готовая бетонная смесь через расходные бункеры А₃ перегружается в транспортные сосуды для доставки к месту бетонирования. При неисправности любого из устройств A_i весь узел останавливается и возобновляет работу после ремонта отказавшего устройства. При этом устройства комплекса, следующие по технологическому процессу после ремонтируемого, сначала принимают дозу материалов или бетонной смеси, находившихся в ремонтируемом устройстве до его аварийной остановки, перерабатывают ее, а затем продолжают рабочий цикл. На основе хронометражных наблюдений нами получены следующие данные, в часах, (таблица 6.4).

Используем аналитический пакет MAPLE.

Исходные данные: А = 2,0; Т = 70,0; R = 16,0; S = 0,5.

Результаты:Количество итераций J = 3.

Начальное значение для поиска «М» М₁ = 1.

Число полных рабочих периодов М = 3.

Коэффициент простоя SK₁ = 0,0228.

Исходные данные: А = 4,0; Т = 100,0; R = 24,0; S = 0,5.

Результаты:Количество итераций J = 2.

Начальное значение для поиска «М» М₁ = 1.

Число полных рабочих периодов М = 2.

Коэффициент простоя SK₁ = 0,0239.

Исходные данные: А = 5,0; Т = 50,0; R = 24,0; S = 1,0.

Результаты:Количество итераций J = 1.

Начальное значение для поиска «М» М₁ = 1.

Число полных рабочих периодов М = 1.

Коэффициент простоя SK₁ = 0,0736.

Отсюда по формуле (6.13) К_п^комп = 0,1550.

Таблица 6.4