Повышение технологической надежности методом резервирования машин
Резервирование горно-проходческих машин и механизмов для транспортного строительства является эффективным методом повышения технологической надежности и производительности труда в строительстве.
Наиболее распространенный случай резервирования - дублированная система, состоящая из двух идентичных восстанавливаемых механизмов. Важным показателем надежности такой системы является коэффициент простоя. Здесь возможны три варианта (рис. 6.7):
а) Технологические перерывы отсутствуют (р = 0) и включенный механизм работает непрерывно до момента его отказа (см. рис. 6.7, а).
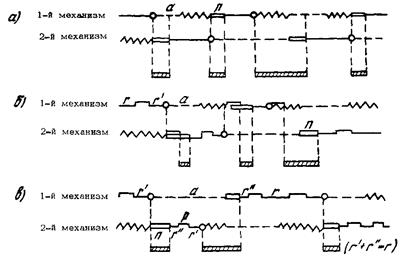
Рис. 6.10. Схема расчета коэффициента простоя оборудования при дублировании механизмов:
 период переключения;
период переключения;  время нахождения в резерве и ожидания ремонта; остальные обозначения см. на рис. 6.6
время нахождения в резерве и ожидания ремонта; остальные обозначения см. на рис. 6.6
Процесс функционирования системы, начиная с 1-го отказа механизма, распадается на статистически однородные интервалы, заключенные между двумя последовательными моментами включения механизмов, находившихся в резерве. Каждый такой интервал J включает период исправного функционирования системы и период ее простоя. Поскольку при t ® ¥ число таких интервалов с вероятностью 1 неограниченно растет, то отношение суммарного времени простоя к суммарному времени работы системы сходится по вероятности к П(J)/Т(J),
где П(J) - математическое ожидание времени простоя на интервале J;
Т(J) - математическое ожидание времени работы на интервале J. Таким образом, Kп = П(J)/Т(J).
Очевидно, что Т(J) = Тср,
где Тср - математическое ожидание времени Т безотказной работы одного механизма. Далее определяется Kп. Можно считать, что t = 0 является началом интервала J. Пусть Q(t) и q(t) - функция и плотность распределения времени безотказной работы механизма, R(t) = 1 - Q(t) - функция надежности механизма, П(t) - математическое ожидание времени простоя системы на J при условии отказа в момент t механизма, включенного при t = 0. Если a - случайная величина (a > П) с плотностью распределения qa(t), то
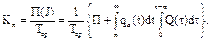 (6.19)
(6.19)
В частности, если a = const, то
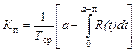 . (6.20)
. (6.20)
При небольших значениях a можно вместо формулы (6.20) использовать приближенную формулу
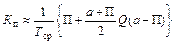 (6.21)
(6.21)
которая получается из формулы (6.20), если принять функцию Q(t) линейной на интервале [0, а-П].
Если значения функции Q(a-П)неизвестно, то значение
 , (6.22)
, (6.22)
получаемое в предположении равномерного распределения Т на интервале [0, Тср].
б) При выходе из строя работающего механизма технологический перерыв начинается в момент его отказа и имеет длительность р¢, пропорциональную предшествовавшему (неполному) рабочему периоду r¢; p¢ = qr¢(рис. 6.9, б). Этот вариант соответствует, в частности, случаю, когда продолжение общего технологического процесса не обусловлено обязательным выполнением всего объема работ, выполняемого данной системой в течение полного рабочего периода r.
Если П > р, аналогично варианту aимеем
П(J)=aQ(ar)+(П+ar)R(ar)-
- 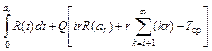 , (6.23)
, (6.23)
где ar - наработка механизма, включенного при t = 0, на интервале [0, a-П] без учета соответствующих перерывов;
i - число полных рабочих периодов, содержащихся в интервале [0, a-П], так что ir £ ar £ (i + 1)r.
Приближенное выражение имеет вид
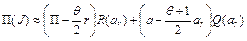 , (6.24)
, (6.24)
а при неизвестных R(ar), Q(ar)
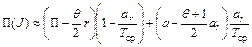 (6.25)
(6.25)
Для случая П < р выражения (6.20) и (6.21) дают оценку сверху, если принять для них П = р.
в) При отказе механизма технологический перерыв делается лишь тогда, когда наработка системы после предшествовавшего перерыва станет равной r - полному рабочему периоду (рис. 6.10, в).
Пусть br - наработка механизма, работающего без отказа, за время восстановления другого механизма, т.е. на интервале [0, a-П]. В этом варианте brслучайна, ar -p £ br £ ar.
Аналогично предыдущему
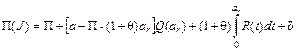 , (6.26)
, (6.26)
где 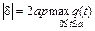 ;
;
Приближенное значение Kпдает соотношение
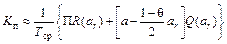 , (6.27)
, (6.27)
а при неизвестной R(ar)
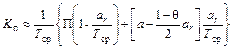 . (6.28)
. (6.28)
Для практических прогнозов часто достаточно использовать приближенные формулы, поскольку и точные формулы не могут отразить всей сложности реального технологического процесса в тоннелестроении.
При проведении работ с использованием различных способов резервирования с целью повышения надежности сложных систем одна из задач - достижение максимальной надежности при данных средствах или двойственная к ней задача - достижение заданной надежности при минимальных затратах средств. В этом случае встает задача оптимального резервирования.
Комплекс горно-проходческого оборудования рассматривается как сложная система, состоящая из некоторых подсистем (ряда машин и механизмов), работающих последовательно, т.е. отказ хотя бы одной из подсистем приводит к отказу всей системы. Тогда вероятность безотказной работы (надежность) системы
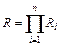 , (6.29)
, (6.29)
где Ri - вероятность безотказной работы i-й подсистемы.
Если машины или механизмы каждой подсистемы резервировать, то, очевидно, Ri = Ri(xi), где xi ³ 0 - количество резервных элементов каждой подсистемы, и тогда
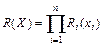 , (6.30)
, (6.30)
где X = x1, x2, … xn - n-мерный вектор.
Требуется найти
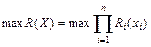 , (6.31)
, (6.31)
при условии, что
 , (6.32)
, (6.32)
где ci - стоимость единицы резервного оборудования i-й подсистемы;
c0 - ограничения на затраты средств.
Эта задача решается методом мажорирующих последовательностей, предложенным Дж. Кеттелем и развитым Ф. Прошаном и Т. Брейем, являющимся модификацией метода динамического программирования. При этом принимается, что каждый элемент i-й подсистемы имеет надежность ri, не зависящую от других элементов этой подсистемы. Тогда 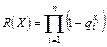 , где qi = 1 - ri и, следовательно, ненадежность системы
, где qi = 1 - ri и, следовательно, ненадежность системы
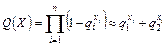 . (6.33)
. (6.33)
При использовании данного метода строится вначале доминирующая последовательность для системы, состоящей из двух подсистем. Для этого составляется таблица с двумя входами (значениями х1 и x2), на пересечении которых указываются c(x1,x2) = c1x1 + c2x2 - стоимость системы с резервными элементами x1и x2и Q(x1,x2)- ненадежность системы.
В таблицу вносятся лишь такие X, которые удовлетворяют условию (6.29). Затем, сравнивая c(x1,x2) и Q(x1,x2), стоящие в таблице, исключают мажорируемые векторы, т.е. такие, для которых в таблице существует по крайней мере один вектор, все координаты которого не превышают по величине координат соответствующего мажорируемого им вектора, причем по крайней мере одна из координат строго меньше. Оставшиеся векторы составляют мажорирующую последовательность. Затем эта мажорирующая последовательность берется в качестве первого входа второй матрицы, а в качестве второго входа берется третья подсистема и описанная процедура повторяется. Таким образом, строится мажорирующая последовательность для системы, содержащей n подсистем. Для уменьшения количества членов мажорирующей последовательности можно ввести допустимую погрешность e по стоимости и допустимую погрешность d по ненадежности. Другим методом сокращения длины мажорирующей последовательности является использование наибольших начальных значений xi0.
Оптимальное количество резервного оборудования можно найти по другому критерию - минимальному коэффициенту простоя, а следовательно, максимальной технологической надежности. Так как
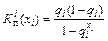 (6.34)
(6.34)
коэффициент простоя для подсистемы, состоящей из механизма Ai и (ni - 1) резервных, то
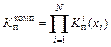 . (6.35)
. (6.35)
Коэффициент простоя всей системы и, значит, Kпкомп можно минимизировать описанным методом доминирующих последовательностей.
Предложенная выше методика может быть применена также для расчетов оптимального количества резервных запасных частей машин и оборудования.
Пусть необходимо, чтобы машина или оборудование функционировали в течение времени (0, t). В случае отказа какой-либо детали она сразу заменяется из числа запасных, если таковая есть. Считается, что нехватка запасных деталей хотя бы одного типа приводит к простою машины, а также, что запасными деталями машина обеспечивается с момента начала ре работы. Рассматриваются два случая:
1. Запасные детали не ремонтируются. Пусть Ri(xi)- вероятность того, что за время функционирования системы потребуется не более xi деталей i-го типа (i = 1, 2,…, n), т.е. что в течение времени t произойдет не более xi отказов деталей (x1, x2, …, xn), то вероятность бесперебойной работы системы в течение времени t будет 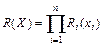 .
.
Если стоимость каждой детали i-го типа ci, общие затраты не должны превышать c0, то имеем ограничения 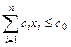 . Задача состоит в выборе значения X, который минимизирует функцию R(X) при наличии линейных ограничений. Следовательно, данная задача сводится к предыдущей.
. Задача состоит в выборе значения X, который минимизирует функцию R(X) при наличии линейных ограничений. Следовательно, данная задача сводится к предыдущей.
Если предположить, что закон распределение времени до отказа деталей i-го типа экспоненциальный, тогда
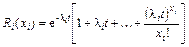 . (6.36)
. (6.36)
2. Запасные детали ремонтируются. В этом случае отказавшая деталь заменяется, если это возможно, запасной. Отказавшая деталь сразу же поступает в ремонт. В машине же непрерывно должно функционировать mi, деталей i-го типа, а в запасе иметься xi деталей того же типа. Каждая из деталей характеризуется экспоненциальным распределением времени работы до отказа, т.е. 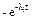 , а распределение времени восстановления произвольно со средним значением mi, причем milimi < 1. Машина не будет работать, если в момент отказа какой-либо детали среди запасных нет соответствующей замены. Это случится тогда, когда отказывает одна из mi функционирующих деталей i-го типа, в то время как все xi запасные детали этого же типа находятся в ремонте.
, а распределение времени восстановления произвольно со средним значением mi, причем milimi < 1. Машина не будет работать, если в момент отказа какой-либо детали среди запасных нет соответствующей замены. Это случится тогда, когда отказывает одна из mi функционирующих деталей i-го типа, в то время как все xi запасные детали этого же типа находятся в ремонте.
Тогда коэффициент готовности, т.е. вероятность того, что машина не будет простаивать из-за того, что отсутствует деталь для замены в момент отказа, определяется по формуле
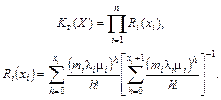 (6.37)
(6.37)
Как и в случае 1, задача состоит в выборе вектора X, максимизирующего Кг(Х) при наличии линейных ограничений 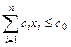 .
.
Дата добавления: 2020-05-20; просмотров: 651;











