Вопрос 2. Статистическое определение вероятности
Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях.
Определение.Вероятностью события A называется число Р(А), около которого колеблется значение статистической частоты этого события при условии увеличения количества испытаний.
При статистическом определении в качестве вероятности события принимается его относительная частота.
Относительной частотой события 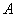 называют отношение числа испытаний
называют отношение числа испытаний 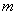 , в которых данное событие появилось, к общему числу
, в которых данное событие появилось, к общему числу 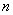 фактически проведённых испытаний:
фактически проведённых испытаний: 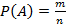 .
.
Частота события обладает следующими свойствами:
1. Частота случайного события есть число, заключенное между нулем и единицей:
0<P(A)<1
2. Частота достоверного события U равна единице:
P(U)=1
3. Частота невозможного события V равна нулю:
P(V)=0
4. Частота суммы двух несовместных событий A и B равна сумме частот этих событий:
P(A+B)=P(A)+P(B)
Пример 1. Из 500 взятых наудачу деталей оказалось 8 бракованных. Найти частоту бракованных деталей.
Решение. Так как в данном случае m = 8, n = 500, то в соответствии с формулой находим
P(A)=8:500=0,016
Пример 2. Игральный кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова частота появления шестерки?
Решение. Из условия задачи следует, что n = 60, m = 10, поэтому
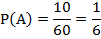
Дата добавления: 2020-04-12; просмотров: 1435;











