Решения дифференциального уравнения
Уравнение для определения функции называется дифференциальным, если в нем участвуют дифференциалы или производные искомой функции. Так, 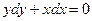 ,
, 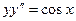 - дифференциальные уравнения, а уравнение
- дифференциальные уравнения, а уравнение 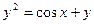 не является дифференциальным.
не является дифференциальным.
Существует два основных типа дифференциальных уравнений: обыкновенные, в которых неизвестная функция зависит только от одного аргумента, и в частных производных, в которые входят производные от искомой функции по нескольким переменным. Уравнения в частных производных мы в этом пособии не будем рассматривать.
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение. Например, 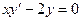 ,
, 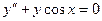 ,
, 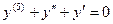 - дифференциальные уравнения соответственно 1-го, 2-го и 5-го порядка.
- дифференциальные уравнения соответственно 1-го, 2-го и 5-го порядка.
Символически дифференциальное уравнение n-го порядка для определения неизвестной функции 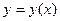 можно записать так:
можно записать так:
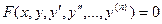 . (1.4)
. (1.4)
(Часто независимый аргумент искомой функции y обозначают через t, а не через x, или другим символом.)
Уравнение (1.4) называется разрешенным относительно старшей производной, если его можно записать в следующем виде:
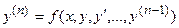 .
.
Решением дифференциального уравнения (1.4) называется такая функция  , которая, будучи подставлена в это уравнение, обращает его в тождество.
, которая, будучи подставлена в это уравнение, обращает его в тождество.
Например, функция x3 является решением уравнения
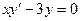 , (1.5)
, (1.5)
так как 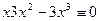 . Аналогично устанавливается, что наряду с функцией x3 решением будет и любая функция вида Сx3, где С - произвольная постоянная величина, а это значит, что уравнение (1.5) имеет бесконечное число решений.
. Аналогично устанавливается, что наряду с функцией x3 решением будет и любая функция вида Сx3, где С - произвольная постоянная величина, а это значит, что уравнение (1.5) имеет бесконечное число решений.
Так же проверяется, что уравнение
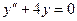 (1.6)
(1.6)
имеет решения вида 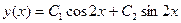 , где C1, C2 – произвольные постоянные.
, где C1, C2 – произвольные постоянные.
В обоих рассмотренных случаях дифференциальное уравнение имеет бесконечное множество решений. Оказывается, что это свойство характерно для всех дифференциальных уравнений: каждое уравнение определяет целое множество (или, как говорят, семейство) решений, зависящее от некоторых числовых параметров, что проявляется в присутствии произвольных постоянных C1, C2,… в решении.
Если число произвольных постоянных, от которых существенно зависит решение, совпадает с порядком уравнения, то найденное семейство решений называется общим решением уравнения. (Это определение мы позже уточним.)
Общее решение может быть задано как в явном ( 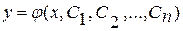 ), так и в неявном виде (
), так и в неявном виде ( 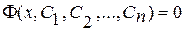 ). В последнем случае оно называется общим интегралом.
). В последнем случае оно называется общим интегралом.
При фиксированных значениях C1, …, Cn , включая 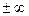 , из общего решения выделяется частное решение (а общий интеграл становится частным интегралом).
, из общего решения выделяется частное решение (а общий интеграл становится частным интегралом).
Например, 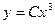 - общее решение уравнения (1.5), а
- общее решение уравнения (1.5), а 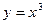 и
и 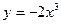 - его частные решения, соответствующие выбору
- его частные решения, соответствующие выбору 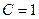 и
и 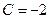 . Общим решением уравнения (1.6), как уже отмечалось, будет
. Общим решением уравнения (1.6), как уже отмечалось, будет 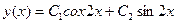 ; его частные решения, получающиеся при выборе
; его частные решения, получающиеся при выборе 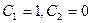 и
и 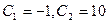 , суть
, суть 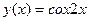 и
и 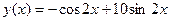 .
.
Наконец, решения, которые нельзя получить из общего, придавая произвольным постоянным определенные значения, называются особыми. Например, общим решением дифференциального уравнения 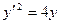 является функция
является функция 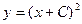 (проверьте!), однако это уравнение имеет еще одно решение
(проверьте!), однако это уравнение имеет еще одно решение 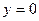 , которое не получается из общего ни при каком значении постоянной С, и значит, является особым. В некоторых случаях именно особые решения дают ответ на поставленный в исследовании вопрос, но задача нахождения особых решений трудна, и мы оставим ее в стороне.
, которое не получается из общего ни при каком значении постоянной С, и значит, является особым. В некоторых случаях именно особые решения дают ответ на поставленный в исследовании вопрос, но задача нахождения особых решений трудна, и мы оставим ее в стороне.
Процесс нахождения решений дифференциального уравнения приводит к необходимости вычислять интегралы, поэтому его называют интегрированием дифференциального уравнения. Когда общий интеграл дифференциального уравнения удается записать в форме, содержащей неопределенные интегралы (пусть даже не выражающиеся через элементарные функции), говорят, что уравнение интегрируется в квадратурах. Следует отметить, что большинство дифференциальных уравнений в квадратурах не интегрируется (один из множества примеров таких уравнений: 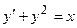 ). В таких случаях решения находят приближенно, например численно, с помощью компьютеров. Однако далее мы рассмотрим некоторые типы уравнений, как раз интегрирующихся в квадратурах.
). В таких случаях решения находят приближенно, например численно, с помощью компьютеров. Однако далее мы рассмотрим некоторые типы уравнений, как раз интегрирующихся в квадратурах.
Целесообразность изучения таких уравнений объясняется несколькими моментами. Во-первых, для осознанного применения приближенных методов нужно разбираться в том, как в принципе получаются точные решения. Во-вторых, при решении задачи можно проследить физические механизмы формирования рассматриваемых процессов и зависимость процессов от параметров. В-третьих, уравнения этого класса очень часто встречаются на практике.
Начальные условия
В большинстве прикладных задач нужно найти функцию, удовлетворяющую как некоторому дифференциальному уравнению, так и некоторым дополнительным условиям. (Совместно, уравнение и эти условия образуют математическую модель исследуемого явления.) Обычно дополнительные условия получают, исходя из физической постановки задачи. Особенно часто задаются условия, определяющие значения решения и его производных при одном и том же значении аргумента, и тогда математическую модель называют задачей Коши.
Пусть, например, нужно получить закон движения тела массы m, брошенного вертикально вверх, под действием силы тяжести. Обозначив через t время, через 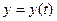 - положение тела, через g – ускорение свободного падения, запишем второй закон Ньютона в проекции на вертикальную ось:
- положение тела, через g – ускорение свободного падения, запишем второй закон Ньютона в проекции на вертикальную ось: 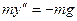 или
или
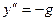 . (1.7)
. (1.7)
Тогда по определению интеграла имеем: 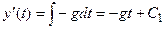 ,
, 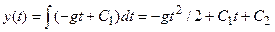 . Мы получили общее решение, которое дает полезную информацию о характере движения тела (квадратичная зависимость высоты от времени), но не позволяет описать его конкретное движение. Для этого в самой формулировке задачи нужны дополнительные условия. Их можно задать различным образом. Пусть, например, в результате измерений установлено, что тело брошено (в момент t=0) из положения y0 со скоростью
. Мы получили общее решение, которое дает полезную информацию о характере движения тела (квадратичная зависимость высоты от времени), но не позволяет описать его конкретное движение. Для этого в самой формулировке задачи нужны дополнительные условия. Их можно задать различным образом. Пусть, например, в результате измерений установлено, что тело брошено (в момент t=0) из положения y0 со скоростью 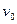 . Эти данные можно выразить так:
. Эти данные можно выразить так:
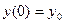 ,
, 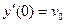 . (1.8)
. (1.8)
Начальные условия (1.8) фиксируют значения постоянных С1, С2: подстановка y(t) в левые части (1.8) дает 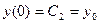 ,
, 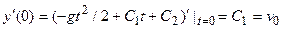 . Тем самым дополнительные условия выделяют из общего решения
. Тем самым дополнительные условия выделяют из общего решения 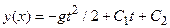 частное
частное 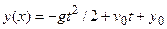 , которое и описывает конкретное движение.
, которое и описывает конкретное движение.
Уравнение (1.7) и условия (1.8) дают пример задачи Коши.
Во многих случаях значения решения и его производных необходимо указывать при разных значениях аргумента x; тогда получается краевая задача. Пример краевой задачи: найти решение уравнения 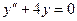 , удовлетворяющего условиям
, удовлетворяющего условиям 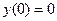 ,
, 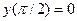 .
.
Также различные дополнительные условия могут использоваться для определения неизвестных параметров задачи. Эти случаи освещаются в разделе 2.6.
Дата добавления: 2020-05-20; просмотров: 592;











