Геометрический смысл дифференциального уравнения и связанных с ним понятий
Пусть 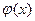 - какое-нибудь решение некоторого дифференциального уравнения 1-го порядка. Равенство
- какое-нибудь решение некоторого дифференциального уравнения 1-го порядка. Равенство  можно считать уравнением некоторой линии на плоскости x, y. Эта линия, т.е. график решения дифференциального уравнения, называется интегральной кривой.
можно считать уравнением некоторой линии на плоскости x, y. Эта линия, т.е. график решения дифференциального уравнения, называется интегральной кривой.
Таким образом, каждое частное (и каждое особое) решение дифференциального уравнения (2.1) геометрически представляет собой некоторую линию – интегральную кривую. Но тогда общее решение 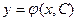 нашего уравнения, являющееся собранием бесконечного множества частных его решений, геометрически представляет собой собрание, или как чаще говорят, однопараметрическое семейство, интегральных кривых: одна кривая этого семейства отличается от другой значением одного параметра – постоянной С.
нашего уравнения, являющееся собранием бесконечного множества частных его решений, геометрически представляет собой собрание, или как чаще говорят, однопараметрическое семейство, интегральных кривых: одна кривая этого семейства отличается от другой значением одного параметра – постоянной С.
Пример 2.1. Рассмотрим уравнение 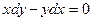 . Преобразуя его к виду
. Преобразуя его к виду 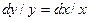 , приравняем интегралы от обеих его частей:
, приравняем интегралы от обеих его частей: 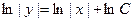 , отсюда
, отсюда 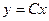 (подробнее о решении этого уравнения см. раздел 2.3). Это семейство прямых, проходящих через начало координат. Параметр С является угловым коэффициентом прямой (рис. 2.1).
(подробнее о решении этого уравнения см. раздел 2.3). Это семейство прямых, проходящих через начало координат. Параметр С является угловым коэффициентом прямой (рис. 2.1).
.Рисунок 2.1
Мы уже знаем, что начальное условие 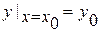 позволяет выделить из общего решения одно-единственное частное. Геометрически же задание такого условия равносильно заданию точки (
позволяет выделить из общего решения одно-единственное частное. Геометрически же задание такого условия равносильно заданию точки ( 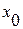 ,
, 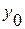 ), через которую обязана пройти соответствующая интегральная кривая. Например, условие
), через которую обязана пройти соответствующая интегральная кривая. Например, условие 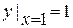 выделяет из семейства интегральных кривых, рассмотренных в нашем примере, т.е. из семейства прямых y=Cx, одну прямую y=x, проходящую через точку (1,1) (рис. 2.1).
выделяет из семейства интегральных кривых, рассмотренных в нашем примере, т.е. из семейства прямых y=Cx, одну прямую y=x, проходящую через точку (1,1) (рис. 2.1).
Остановимся теперь на вопросе о том, что геометрически выражает само дифференциальное уравнение первого порядка. Пусть  -то частное решение, которое удовлетворяет начальному условию
-то частное решение, которое удовлетворяет начальному условию 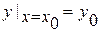 , т.е. та интегральная кривая уравнения (2.1)
, т.е. та интегральная кривая уравнения (2.1) 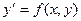 , которая проходит через точку (
, которая проходит через точку ( 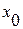 ,
, 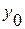 ). Оказывается, что можно очень просто найти угловой коэффициент касательной к интегральной кривой в каждой точке, даже не зная самого решения
). Оказывается, что можно очень просто найти угловой коэффициент касательной к интегральной кривой в каждой точке, даже не зная самого решения  . Действительно, упомянутый угловой коэффициент в точке (
. Действительно, упомянутый угловой коэффициент в точке ( 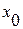 ,
, 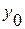 ) равен
) равен 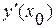 , но так как
, но так как 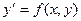 , то
, то 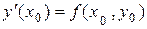 .
.
Таким образом, тангенс угла наклона касательной 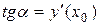 к интегральной кривой в точке (
к интегральной кривой в точке ( 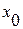 ,
, 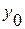 ) равен
) равен 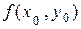 .
.
Каждая касательная задает некоторое направление, которое удобно изображать следующим образом. В точках области, в которых определена функция 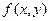 , проведем вектор единичной длины, образующий с осью Оx угол arctg
, проведем вектор единичной длины, образующий с осью Оx угол arctg 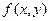 (положительное направление вектора можно взять произвольным). Полученная в результате совокупность указателей называется полем направлений.
(положительное направление вектора можно взять произвольным). Полученная в результате совокупность указателей называется полем направлений.
Если теперь построить поле направлений, достаточно густо нанеся указатели, и провести кривые, касательные к которым совпадают с указателями поля направлений в каждой точке, то эти кривые приближенно являются интегральными кривыми уравнения.
Поле направлений удобно строить не хаотично, а выбирать точки (x,y), в которых указатели имеют одинаковое направление, т.е. 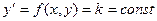 . Линии, образованные такими точками, называются изоклинами, а описанное выше построение интегральных кривых – методом изоклин.
. Линии, образованные такими точками, называются изоклинами, а описанное выше построение интегральных кривых – методом изоклин.
На рисунке 2.2 изображено поле направлений, определяемое дифференциальным уравнением 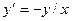 . Уравнения изоклин:
. Уравнения изоклин: 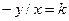 или
или 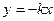 . Это семейство прямых. По полю направлений приближенно строятся интегральные кривые. Можно убедиться. что они соответствуют точным решениям
. Это семейство прямых. По полю направлений приближенно строятся интегральные кривые. Можно убедиться. что они соответствуют точным решениям 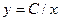 , определяющим гиперболы.
, определяющим гиперболы.
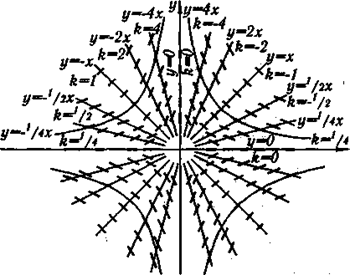
Рисунок 2.2.
Дата добавления: 2020-05-20; просмотров: 756;











