Цилиндрически-симметрическое распределение зарядов.

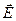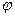Решим задачу об определении и для бесконечного цилиндра радиуса R, заряженного с объемной плотностью

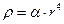(7.1)

Ось цилиндра совмещена с осью z, r - цилиндрическая радиальная координата. Те же рассуждения о симметрии, которые были сделаны в начале §6, приводят к тому, что цилиндрически-симметричное поле 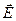имеет вид:

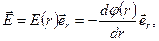(7.2)

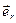- орт, касательный к цилиндрической радиальной координатной линии.

Для того, чтобы иметь дело с конечным значением полного заряда в теореме Гаусса, рассмотрим область трехмерного пространства, ограниченную плоскостями z = 0 и z = H.

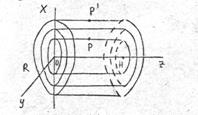
Рис.8

а) Найдем 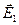- внутри цилиндра радиуса R. Через точку Р во внутренней области заряженного цилиндра проведем цилиндрическую поверхность радиуса r < R. Для полученного цилиндра радиуса r и высоты H можно применить теорему Гаусса

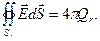(7.3)

Используя второе основное свойство поверхностного интеграла (5.5), получаем, что интеграл по замкнутой поверхности в (7.3) разлагается на сумму трех интегралов: по первому и второму основаниям и по боковой поверхности вырезанного нами цилиндра

(*)

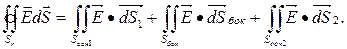Нормали к основаниям направлены параллельно оси z, а нормаль к боковой поверхности параллельна 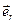. Поэтому из формулы для векторного элемента поверхности в цилиндрической системе координат (4.12) следует, что

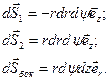(7.4)

Из (7.2) и (7.4) видно, что

(*)

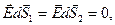
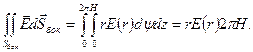Легко видеть, что

(**)

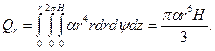Подставляя последние два результата в теорему Гаусса (7.3) получаем

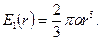(7.5)

б) Найдем 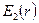вне цилиндра аналогичным способом. Используем теорему Гаусса для цилиндра высоты Н и радиуса r < R. Вместо (**) имеем

(***)

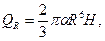окончательно

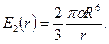(7.6)

в) Найдем потенциал внутри 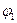и вне 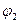заряженного цилиндра. Во внутренней области из (7.2) и (7.5) получаем

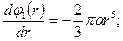
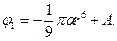(7.7)

Для определения постоянной интегрирования А положим

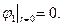
Отсюда следует, что А обращается в нуль. Для внешней области имеем

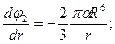
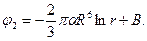(7.8)

Постоянная интегрирования В получается из условия «сшивания» внешнего и внутреннего решений:

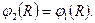(7.9)

Окончательно имеем, что

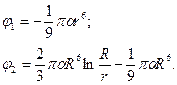(7.10)