Натуральный репер, присоединенный к криволинейной системе координат.
Сферическая система координат определяется формулами:
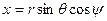 ;
;
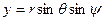 (2.1)
(2.1)
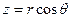
На примере сферических координат введем понятие координатных линий, которое вводится тем же способом для всех других систем координат.
Рассмотрим произвольную точку 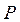 , положение которой определяется значениями
, положение которой определяется значениями 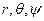 . Координатная линия
. Координатная линия 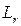 получается движением точки
получается движением точки 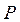 при постоянных
при постоянных 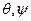 . Линии
. Линии 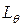 и
и 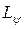 получаются изменениями
получаются изменениями 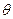 и
и 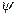 при фиксированных значениях остальных координат.
при фиксированных значениях остальных координат.
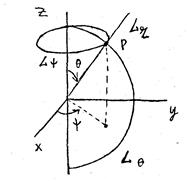
Рис.3
Формулы перехода к общим криволинейным координатам 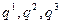 имеют аналогичный вид:
имеют аналогичный вид:
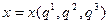
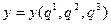 (2.2)
(2.2)
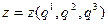
Подставляя эти формулы в (1.1), видим, что в общем случае радиус-вектор точки 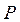 является сложной функцией от криволинейных координат:
является сложной функцией от криволинейных координат:
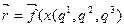 ,
, 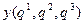 ,
, 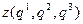 ) =
) = 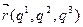 . (2.3)
. (2.3)
От точки 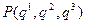 сместимся вдоль координатной линии
сместимся вдоль координатной линии 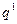 , придавая только этой координате приращение
, придавая только этой координате приращение 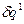 . Получаемый при этом вектор
. Получаемый при этом вектор 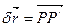 направлен вдоль координатной линии
направлен вдоль координатной линии 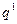 .
.
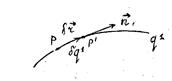
Рис.4
Следовательно, существует такой конечный вектор 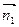 , касательный к координатной линии
, касательный к координатной линии 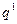 в точке
в точке 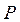 , что имеет место уравнение:
, что имеет место уравнение:
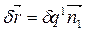 . (2.5)
. (2.5)
Аналогичные соотношения получаются и вдоль координатных линий:
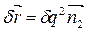 ;
; 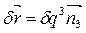 (2.6)
(2.6)
Следовательно, векторный элемент длины в криволинейной системе координат определяется формулой:
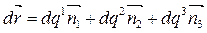 . (2.7)
. (2.7)
Из (2.5) и (2.6) следует, что
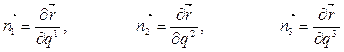 . (2.8)
. (2.8)
Таким образом, имеется тройка векторов 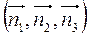 с общим началом и касательных в каждой точке пространства координатным линиям
с общим началом и касательных в каждой точке пространства координатным линиям 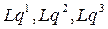 . Векторные поля
. Векторные поля 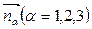 образуют поле натурального репера, присоединенного к криволинейной системе координат
образуют поле натурального репера, присоединенного к криволинейной системе координат 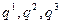 .
.
Если применить правило дифференцирования сложной функции от многих переменных к (2.8), учитывая (2.3), то получаются формулы перехода от декартова репера к натуральному реперу:
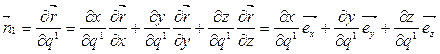 ;
;
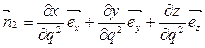 ;
;
(2.9)
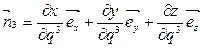 .
.
Эти формулы для сферических координат имеют вид:
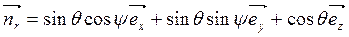 ;
;
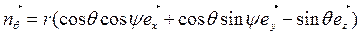 ; (2.10)
; (2.10)
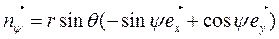 .
.
А для цилиндрической системы
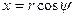 ,
, 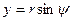 ,
, 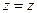 . (2.11)
. (2.11)
имеем:
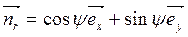 ;
;
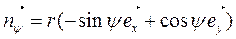 (2.12)
(2.12)
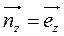 .
.
Дата добавления: 2016-06-22; просмотров: 1653;











