Применение дельта-функции Дирака и ступенчатой функции для описания распределения объемной плотности тока

Объемные плотности заряда и тока для случаев типа распределения зарядов по поверхности, линии и других ограниченных областей записываются в виде скалярной и векторной функций, определенных во всем трехмерном пространстве. Свойства дельта-функции и ступенчатой функции и их применение даны в задачнике [1]. Желательно прорешать задачи 80,81,88 и проработать приложения о свойствах указанных обобщенных функций в [1].

Разберем подробно решения двух задач из [1].

149 г): В плоскости ху по бесконечно тонкому кольцу радиуса R течет линейный ток J, образуя правовинтовую систему с осью z, которая проходит через центр кольца. Используя дельта-функцию Дирака определить распределение объемной плотности тока .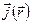

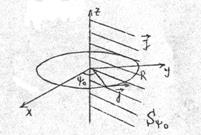
Рис.10

Решение: Некоторое значение азимутального угла 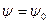определяет плоскость . Согласно определению понятия силы тока имеем нормировочное условие для искомой объемной плотности тока:

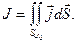(9.1)

Плотность тока отлична от нуля при следующих значениях цилиндрических координат:

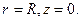(9.2)

Поэтому вектор объемной плотности тока нужно искать в виде:

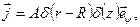(9.3)

А - нормировочный множитель.

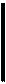В силу того, что

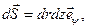(9.4)

получаем

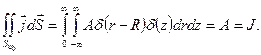(9.5)

Задача решена.

149 д): Найти 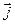, если равномерно заряженная с поверхностной плотностью 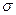поверхность кругового конуса с вершиной в начале координат вращается вокруг своего диаметра с угловой скоростью 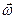, направленной вдоль оси z.

Решение: Известно, что

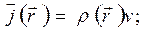(9.6)

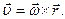(9.7)

Поэтому сначала найдем распределение объемной плотности заряда 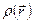. Очевидно, что в сферической системе координат

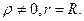(9.8)

Следовательно,

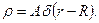(9.9)

Нормировочный множитель А найдем из условия:

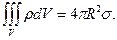(9.10)

Вычислив объемный интеграл в этой формуле по всему трехмерному пространству получим, что

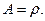(9.11)

Найдем результат векторного произведения (9.7) в сферической системе координат.

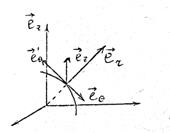
Рис.11

Пусть

(*)

тогда

(**)

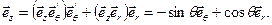Легко видеть, что

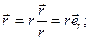(9.12)

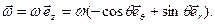(9.13)

В силу взаимной ортогональности базисных ортов сферической системы координат для них имеет место следующая таблица векторных произведений:

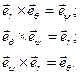(9.14)

Следовательно,

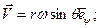(9.15)

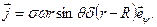(9.16)

Задача решена.

Закон Био-Савара

Распределения объемных плотностей тока, типа полученных выше формул, позволяют сводить к квадратурам задачу об определении компонент вектора напряженности магнитного поля на основе закона Био-Савара:

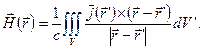(10.1)

Найти напряженность магнитного поля в вакууме, создаваемое током, силы I, текущим по прямому тонкому проводу бесконечной длины.

Решение:Ось z цилиндрической системы координат совместим с проводом.

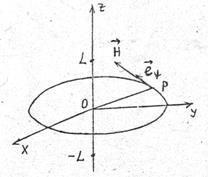
Рис.12

Используя нормировочное условие

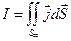(10.2)

и очевидное соотношение

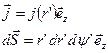(10.3)

найдем, что

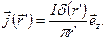(10.4)

Рассмотрим точку Р с координатами 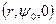. Вычислим 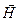, создаваемое участком .

Предельный переход даст поле бесконечного провода, которое обладает осевой симметрией относительно вращений (вокруг оси z) и трансляционной симметрией для сдвигов по оси z.

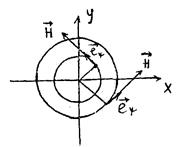
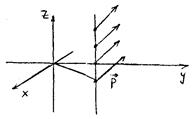
Рис.13

Радиус-вектор 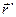положения элемента объема 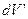в интеграле (10.1) пробегает все трехмерное пространство:

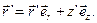(10.5)

Точка наблюдения Р определяется радиус-вектором:

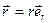(10.6)

Отсюда следует, что

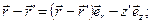(10.7)

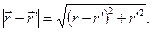(10.8)

Таблица векторных произведений базисных ортов цилиндрической системы координат имеет вид:

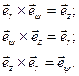(10.9)

Следовательно,

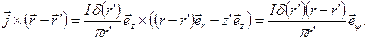(10.10)

Подставим все полученные результаты в формулу (10.1) и получаем

(*)

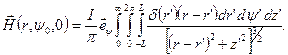Учтем, что

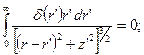
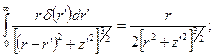
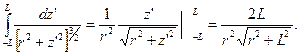
Окончательно, имеем

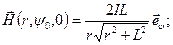(10.11)

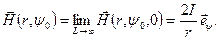(10.12)

Задача решена.

Теория потенциала

11.1 Метод частного интегрирования

11.1.1. Представление неопределенного интеграла как обратного оператора для дифференцирования функции

Любой известной функции 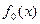от одного переменного можно сопоставить её производную, равную пределу

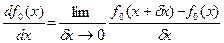. (11.1)

Значение производной является новой функцией, которую обозначим следующим образом

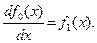(11.2)

Можно сформулировать обратную задачу: по заданной функции 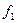найти такую функцию 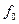, которая удовлетворяет уравнению (11.2). Последняя функция в математическом анализе называется первообразной исходной функции 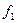. Умножая уравнение (11.2) на дифференциал аргумента получим эквивалентную форму этого дифференциального уравнения как равенство бесконечно малых величин первого порядка

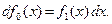(11.3)

Введем оператор интеграла как обратное к дифференциалу действие на функцию

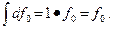(11.4)

Можно написать символическое уравнение для взаимно обратных и перестановочных операторов интегрирования и дифференцирования

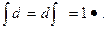(11.5)

Умножая (11.3) на оператор интегрирования получаем соотношение

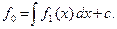(11.6)

Последнее слагаемое, равное произвольной постоянной, при дифференцировании этого соотношения исчезает. Оно известно как константа интегрирования. Подстановка (11.6) превращает (11.3) в тождество и поэтому она является общим решением дифференциального уравнения (11.3). Здесь «дифференциальным» называем уравнение, содержащее символы дифференцирования неизвестной функции. Покажем, что (11.6) удовлетворяет уравнению (11.2)

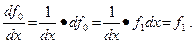(11.7)

Отсюда следует, что оператор полной производной и неопределенный интеграл от функции взаимно обратны

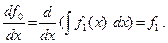(11.8)

Символические вычисления позволяет доказать перестановочность этих двух операций

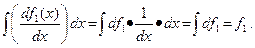(11.9)

Литература

1. Алексеев А.Н. Сборник задач по классической электродинамике. М.: Наука, 1977.