Закон Ома для замкнутой цепи. Правила Кирхгофа
Если квазилинейный ток замкнут, то, применяя к нему формулу (5), получим закон Ома для замкнутой цепи
IR = e, (6)
где e – полная ЭДС в рассматриваемой цепи (равная, очевидно, алгебраической сумме всех ЭДС на каждом его участке). Таким образом, ток в замкнутой цепи определяется (помимо ее сопротивления R) лишь действующими в ней сторонними силами и не зависит от распределения потенциала вдоль нее. Физически исчезновение члена 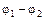 в (5) при переходе к замкнутому контуру обусловлено потенциальностью электрического поля. Ведь разность потенциалов между концами любого отрезка пропорциональна работе сил поля на этом отрезке, и, если он замкнут, должна, конечно, обратиться в нуль.
в (5) при переходе к замкнутому контуру обусловлено потенциальностью электрического поля. Ведь разность потенциалов между концами любого отрезка пропорциональна работе сил поля на этом отрезке, и, если он замкнут, должна, конечно, обратиться в нуль.
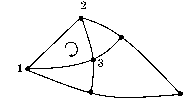 Рис. 2 Рис. 2
|
Рассмотрим теперь произвольную цепь с разветвлениями, состоящую из участков, на каждом из которых текут (вообще говоря, разные) квазилинейные токи (рис. 2). Составим из таких участков какой-либо замкнутый контур (например 1 – 2 – 3 – 1) и выберем произвольно положительное направление его обхода, которое задаст положительные направления на каждом его участке. Записывая для этих участков обобщенный закон Ома (5), получим
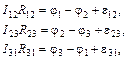
где 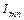 – ток, текущий по участку mn (взятый с соответствующим знаком). Суммирование этих уравнений с заменой обозначений дает
– ток, текущий по участку mn (взятый с соответствующим знаком). Суммирование этих уравнений с заменой обозначений дает
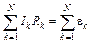 , (7)
, (7)
где 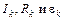 – соответственно ток, сопротивление и ЭДС, отнесенные к каждому участку, а N – их число в контуре. Разности потенциалов, существующие на отдельных участках, при сложении вдоль замкнутого контура, очевидно, и здесь взаимно уничтожатся ввиду потенциального характера электростатического поля. Соотношение (7) называется вторым правилом (или законом) Кирхгофа. Оно утверждает, что в любом замкнутом контуре алгебраическая сумма произведений типа
– соответственно ток, сопротивление и ЭДС, отнесенные к каждому участку, а N – их число в контуре. Разности потенциалов, существующие на отдельных участках, при сложении вдоль замкнутого контура, очевидно, и здесь взаимно уничтожатся ввиду потенциального характера электростатического поля. Соотношение (7) называется вторым правилом (или законом) Кирхгофа. Оно утверждает, что в любом замкнутом контуре алгебраическая сумма произведений типа 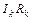 равна сумме (тоже алгебраической) сторонних ЭДС, действующих на этом контуре. Нетрудно видеть, что закон Ома для замкнутой цепи (6) есть частный случай правила Кирхгофа (7), когда токи во всех участках контура одинаковые.
равна сумме (тоже алгебраической) сторонних ЭДС, действующих на этом контуре. Нетрудно видеть, что закон Ома для замкнутой цепи (6) есть частный случай правила Кирхгофа (7), когда токи во всех участках контура одинаковые.
 Рис. 3.
Рис. 3.
|
Первое правило (закон) Кирхгофа является прямым следствием условия стационарности токов (18л14) и относится к узлам, т. е. точкам разветвления токов (рис. 3). Окружая узел произвольной замкнутой поверхностью S и записывая поток вектора j (т. е. полный ток) через нее как алгебраическую сумму пересекающих ее квазилинейных токов, получим
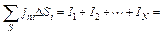
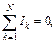 (8)
(8)
где вытекающие токи (как дающие положительный вклад в поток) считаются положительными, а втекающие – отрицательными. Это выражение и представляет собой содержание 1 закона Кирхгофа: алгебраическая сумма токов, вытекающих из любого узла, равна нулю.
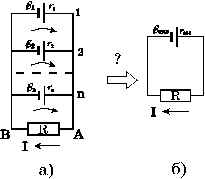 Рис. 4.
Рис. 4.
|
Применяя 1 и 2 правила Кирхгофа к различным контурам и узлам произвольной разветвленной цепи, можно всегда найти токи, текущие по любому ее участку, зная которые нетрудно получить (используя обобщенный закон Ома (5)) и напряжения на каждом из них.
В качестве примера рассмотрим батарею параллельно соединенных источников ЭДС, включенных на некоторое сопротивление нагрузки R (рис. 4 а)[12], и зададимся вопросом, может ли она быть заменена одним эквивалентным источником, и если да, то как найти его ЭДС 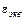 и внутреннее сопротивление
и внутреннее сопротивление 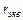 ?
?
Для ответа на этот вопрос напишем второй закон Кирхгофа сначала для контура, образованного источником 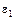 и нагрузкой R, выбрав направление его обхода, как указано на рис. 4 а, и пренебрегая сопротивлением соединительных проводов:
и нагрузкой R, выбрав направление его обхода, как указано на рис. 4 а, и пренебрегая сопротивлением соединительных проводов:
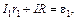
где 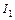 – ток через элемент
– ток через элемент 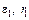 – его внутреннее сопротивление, а I – ток во внешней цепи (через R). Разделив это соотношение на
– его внутреннее сопротивление, а I – ток во внешней цепи (через R). Разделив это соотношение на 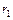 , получим
, получим
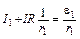 .
.
Напишем теперь аналогичные выражения для контуров 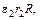
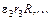 ,
, 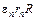 и сложим их все:
и сложим их все:
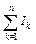 +
+ 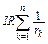 =
= 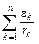 . (9)
. (9)
Но по первому правилу Кирхгофа, примененному к узлу A (точки 1, 2, ... n , А можно, очевидно, считать одной точкой – ведь они соединены проводниками, не имеющими сопротивлений),
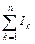 = I,
= I,
так что (9) примет вид
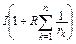 =
= 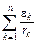 . (10)
. (10)
Если замена рассматриваемой батареи одним источником возможна, то (10) должно быть эквивалентно закону Ома для замкнутой цепи рис. 4 б
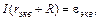
или
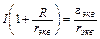 . (11)
. (11)
Сравнивая (10) и (11), заключаем, что они тождественно совпадут, если
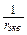 =
= 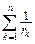 , (12)
, (12)
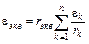 . (13)
. (13)
Итак, замена возможна, причем параметры эквивалентного элемента даются формулами (12) и (13). Впрочем, как явствует из приведенных рассуждений, эквивалентность эта справедлива только по отношению к внешней цепи, которая никак не «почувствует» замены, ибо значения тока и напряжения в ней сохранятся. Что же касается мощности, выделяемой внутри батареи и эквивалентного источника, то, как мы увидим в следующем параграфе, схемы эти отнюдь не равноценны. Это понятно уже из того факта, что при размыкании внешней цепи в схеме рис. 4 б исчезает ток, в то время как в батарее рис. 4 а останутся внутренние токи, приводящие даже в случае разомкнутой внешней цепи к выделению тепла.
Найденные параметры эквивалентного источника позволяют без труда полностью описать процессы в схеме рис. 4 а. Определим, например, напряжение и ток, текущий в k-том элементе.
Во внешней цепи сторонних сил нет, а потому по закону Ома (3л14)
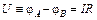 .
.
Но в соответствии с (6)
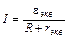 ,
,
стало быть,
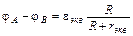 .
.
Для вычисления тока через k-тый элемент, где уже действуют сторонние силы, применим обобщенный закон Ома (5)
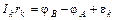
(напряжение сменило знак, потому что мы любой участок цепи проходим по часовой стрелке, в соответствии с выбранными на рис. 4 а направлениями обхода контуров), откуда
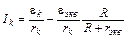 .
.
Дата добавления: 2016-06-22; просмотров: 2311;











