Закон Био – Савара. Принцип суперпозиции

Определение магнитного поля (5), по существу, наполняется физическим содержанием лишь после того, как будет описано, каким образом оно возбуждается текущими токами. Ведь экспериментально проверяется именно действие тока на ток, и без этого описания определение (5) «повисает в воздухе».

Следуя аналогии с электростатикой, мы должны теперь сформулировать закон (аналогичный закону Кулона для поля), позволяющий рассчитать магнитное поле, создаваемое в любой точке пространства (в вакууме) данным элементом линейного тока. Однако, оставаясь в рамках магнитостатики, этого сделать нельзя, ибо, как уже отмечалось, любая цепь постоянного тока замкнута и отдельного элемента такого тока не существует. Таким образом, мы всегда имеем дело с результирующим полем всех элементов этой цепи, а знания результирующей недостаточно для однозначного определения составляющих.

Тем не менее, выходя за эти рамки, т. е. оперируя с переменными токами, могущими быть незамкнутыми и, таким образом, составлять отдельный элемент тока, все-таки удается сформулировать (и экспериментально подтвердить) интересующий нас закон. Он носит название закона Био – Савара[20] и выглядит (в системе СИ) следующим образом:

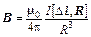, (8)

где R – радиус-вектор, проведенный из (любой) точки элемента тока IDl в точку наблюдения, где этим током создается поле B, а m₀ = 4p × 10^–7 ед. СИ – размерный коэффициент, называемый магнитной постоянной[21].

Из этого закона следует, что поле элемента по величине

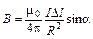(9)

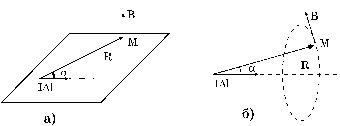Рис. 4.

при удалении от него вдоль какой-либо прямой убывает (как и поле точечного заряда) обратно пропорционально квадрату расстояния до этого элемента, но, во-первых, зависит от его ориентации и, во-вторых, всегда перпендикулярно ему (рис. 4 а). Если фиксировать R и менять a, т. е. перемещаться по сфере радиуса R с центром в Dl, то величина индукции будет меняться пропорционально синусу угла между Dl и направлением на точку наблюдения M, достигая максимального значения в точках плоскости, проходящей через Dl и перпендикулярной ему, и обращаясь в нуль на оси тока. Если фиксировать и R, и a, то получим геометрическое место точек равной величины B, которое, очевидно, представляет собой окружность с центром на оси тока, перпендикулярную этой оси (рис. 4 б). В каждой точке этой окружности вектор B касателен к ней, а потому она представляет собой линию вектора магнитной индукции B. Таким образом, линии B малого элемента тока являются окружностями, перпендикулярными его оси и нанизанными на нее своими центрами, причем направление этих линий образует с направлением тока правовинтовую систему.

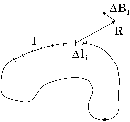Рис. 5.

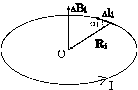Рис. 6.

Имея формулу (8) для расчета поля малого элемента тока, можно найти поле произвольного тока или системы токов. Для этого необходимо разбить все эти токи на малые элементы, посчитать поле каждого элемента и затем их векторно сложить. При этом, однако, весьма существенным оказывается вопрос: как поле отдельного элемента, даваемое законом Био – Савара, искажается присутствием остальных элементов? Никак, гласит ответ, полученный из эксперимента, данный элемент в любых условиях создает одно и то же поле (8). Таким образом, так же, как и в электростатике, здесь выполняется принцип суперпозиции, согласно которому поля, возбуждаемые отдельными элементами, не влияют друг на друга, а лишь накладываются, векторно суммируясь вкаждой точке. Стало быть, вклады каждого элемента произвольной цепи (рис. 5) в общее поле Внужно считать по формуле (8), так что

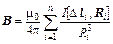, (10)

где суммирование производится по всем участкам, на которые разбит линейный ток I.

Пример. Найти индукцию магнитного поля в центре кольца радиуса R, несущего линейный ток I (рис. 6). Разобьем кольцо на маленькие отрезки Dl_i и посчитаем вклад 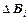каждого из них в искомое поле. Очевидно, все 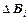будут перпендикулярны плоскости кольца и направлены на рис. 6 вверх. Абсолютная величина 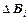в соответствии с (9)

= ,

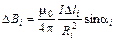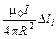ибо все 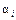= p / 2 и все 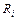= R. Суммируя вклады всех участков кольца, получим

B = = = .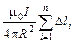

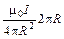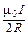Отметим, что по направлению вектор B образует с направлением тока в кольце правовинтовую систему.