Взаимодействие элементов тока

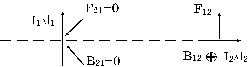Рис. 7.

Комбинируя определение магнитного поля (5) и закон Био – Савара (8), можно получить выражение для силы взаимодействия двух произвольно ориентированных элементов тока (аналогичное закону Кулона в электростатике). Выражение это оказывается, однако, довольно громоздким, ибо в него войдет двойное векторное произведение, которое заметно не упрощается. В то же время для анализа возникающих при таком взаимодействии нюансов нам достаточно рассмотреть его частный случай взаимно перпендикулярных элементов, один из которых лежит на оси другого (рис. 7).

Поскольку элемент I₁Dl₁ находится на оси элемента I₂Dl₂ , последний не возбуждает поле в месте нахождения первого и, следовательно, элемент I₁Dl₁ никакой силы со стороны I₂Dl₂ испытывать не будет (F₂₁ = 0). Элемент же I₂Dl₂, напротив, лежит в перпендикулярной к току I₁Dl₁ и пересекающей его плоскости, т. е. там, где его поле как раз максимально (sin a = 1). Индукция поля B₁₂ этого тока направлена на рис. 7 от нас, и элемент 2 будет испытывать силу F₁₂ , действующую вверх. Таким образом,

F₁₂ ¹ – F₂₁

и налицо явное нарушение третьего закона Ньютона. В чем же здесь дело?

Мы пришли к этому противоречию потому, что незаметно встали на точку зрения дальнодействия. Ведь перейдя к взаимодействию элементов друг с другом, мы исключили из рассмотрения весьма существенный физический объект – магнитное поле, а этого делать нельзя. В том, что третий закон Ньютона здесь не выполняется, ничего удивительного нет: ведь если рассматривать его в рамках дальнодействия (т. е. в формулировке, данной в § 2.3), то он в определенных ситуациях может и даже должен нарушаться. Рассмотренный пример этого нарушения является еще одной иллюстрацией[22] несостоятельности теории дальнодействия.

Если же встать на точку зрения близкодействия и включить в рассмотрение возбуждаемое токами магнитное поле, то полученное противоречие может быть устранено. С точки зрения близкодействия элемент I₂Dl₂ взаимодействует не с элементом I₁Dl₁, а с его полем. «Ощущая» со стороны этого поля силу F₁₂ , он, в свою очередь, образно говоря, сам «действует на него» с равной и противоположной силой «отдачи», что проявляется в изменении импульса поля[23]. Можно строго показать, что при любых взаимодействиях зарядов и токов полный (т. е. механический и электромагнитный) импульс замкнутой системы сохраняется. Поскольку закон сохранения импульса полностью эквивалентен третьему закону Ньютона (в его обобщенной форме, включая в рассмотрение поле), то этим и устраняется указанное противоречие.

А если взаимодействуют два замкнутых постоянных тока? И электрическое, и магнитное поля таких токов стационарны, т. е. со временем не меняются. Не может измениться, следовательно, и электромагнитный импульс этого поля. Тем не менее, и в этом случае третий закон выполняется, только применять его надо уже не к отдельным элементам тока, а в целом к контурам. Ведь как уже отмечалось, в этом случае экспериментально невозможно из результирующего поля каждого контура выделить вклады отдельных его элементов, а потому опытной проверке подлежит лишь силовое воздействие на токи этого суммарного поля. Расчеты же показывают, что для двух произвольных контуров суммирование сил попарного взаимодействия их элементов (полученных из (5) и (8)) всегда дает результирующие силы, удовлетворяющие третьему закону Ньютона. Таким образом, отмеченное кажущееся противоречие не опровергает, а лишний раз подтверждает описанный нами механизм магнитного взаимодействия токов.

Контрольные вопросы и задания

1. Что называется векторным произведением векторов. Коммутативно ли оно?

2. Дать определение вектора индукции магнитного поля. Почему его определение через момент сил, действующих на рамку с током, не вполне корректно?

3. Дать название и определение единицы магнитного поля.

4. Сформулировать правило левой руки.

5. Можно ли в рамках магнитостатики экспериментально определить силу, испытываемую малым элементом постоянного тока? Если да, то как именно, если нет – почему?

6. Сформулировать закон Био – Савара. Как меняется поле малого элемента тока при удалении от него по разным направлениям точки наблюдения? Что представляет собой линия В элемента тока?

7. Можно ли в рамках магнитостатики экспериментально определить поле, созданное малым элементом постоянного тока? Если да, то как именно, если нет – почему?

8. Сформулировать принцип суперпозиции полей в магнитостатике.

9. Каким требованиям должен удовлетворять «пробный» элемент тока?

10. Найти поле в центре кругового тока.

11. Удовлетворяют ли третьему закону Ньютона силы взаимодействия двух элементов тока? Двух замкнутых постоянных токов?

Лекция 17

Основные уравнения магнитостатики

Для магнитного поля постоянных токов могут быть получены уравнения, аналогичные электростатическим (7л11). Уравнения эти выводятся из закона Био – Савара и принципа суперпозиции (и в свою очередь влекут за собой их выполнение). Поскольку, однако, закон Био – Савара существенно сложнее своего электростатического аналога, вывод уравнений магнитостатики выходит за пределы того математического аппарата, которым мы владеем. Нам под силу оказывается лишь доказательство одного из них, и то для частного случая прямых бесконечных токов.