Шаг младенца – шаг великана.
В открытой литературе этот метод впервые был описан Шенксом (Daniel Shanks), ссылки на него известны с 1973 года. Это был один из первых методов, более быстрый чем метод прямого перебора.
Общая схема алгоритма такова:
Берем два целых числа m и k, таких что mk>p (как правило, m=k= 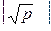 ). Затем вычисляются два ряда чисел:
). Затем вычисляются два ряда чисел:
a, ga, g2a, … , gm—1a (mod p)
gm, g2m, g3m, … , gkm (mod p)
(все вычисления произведены по модулю p).
Найдем такие i и j, для которых gia=gjm. Тогда x=jm—i.
Справедливость последнего равенства подтверждается следующей цепочкой, все вычисления в которой произведены по модулю p:
gx=gjm-i=gjm(gi)-1=gjma(gia)-1=gjma(gjm)-1=a.
Заметим, что числа i и j непременно будут найдены, поскольку при i= 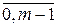 , j=
, j= 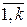 выполняется jm—i=
выполняется jm—i= 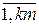 , причем km>p. То есть среди всех чисел вида jm—i обязательно содержится 0 < x ≤ p.
, причем km>p. То есть среди всех чисел вида jm—i обязательно содержится 0 < x ≤ p.
Замечание: Указанный метод можно применять для разыскания дискретных логарифмов в любой циклической группе порядка n.
Приведем этот метод в форме алгоритма.
Алгоритм «Шаг младенца-шаг великана»:
Вход: g - порождающий элемент конечной группы G порядка n; a 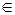 G.
G.
Ш.1. Вычислить m= 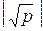 .
.
Ш.2. Вычислить b=gm.
Ш.3. Вычислить последовательности ui=bi, vj=agj Для i,j= 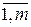 .
.
Ш.4. Найти i, j такие что ui=vj. x=mi—j mod n. Идти на Выход.
Выход: logga=x.
Одна из трудоемких частей этого алгоритма – это поиск на Шаге 4. Он может быть осуществлен несколькими способами:
1) Сначала построить таблицу (i, ui), отсортировать ее по второй компоненте а затем произволить сравнения по мере нахождения компонент vj.
2) Построить две таблицы (i, ui) и (j, vj), отсортировать каждую из них, а затем произвести поиск совпадений.
3) Объединить u, v в одну таблицу, снабдив их номером в соответствующей последовательности и битом принадлежности к одной из двух последовательностей, а затем применить совместную сортировку. И т. п.
Сложность данного алгоритма составляет O( 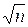 ) умножений по модулю и O(
) умножений по модулю и O( 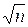 log n) операций сравнения.
log n) операций сравнения.
Пример.
Пусть n=229 (простое число), g=6, a=12.
Ш.1. m=16.
Ш.2. b=ga mod n =612 mod 229 = 183.
Ш.3. В этом примере вычислим сначала ряд ui, а затем будем вычислять компоненты vj до тех пор, пока не найдется совпадение.
| i, j | ||||||||||
| ui | ||||||||||
| vj | 196 |
| 196 | |||||
i=16, j=6. x=mi—j mod n = 250 mod 228 = 22.
Проверка: 622 mod 229= 12.
Ответ: log612 mod 228 = 22.
Дата добавления: 2018-11-26; просмотров: 4278;











