Методы случайных квадратов.
Пусть n – нечетное составное число, не являющееся степенью целого числа. Методы случайных квадратов – это группа методов, основанная на следующей идее:
Пусть n – нечетное составное число, не являющееся степенью целого числа. Целые x, y – такие случайные числа, что x2≡y2(mod n), x 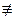 ±y(mod n). Тогда n\(x2—y2), но n не делит ни (x+y), ни (x—y), а значит НОД(x—y,n) – нетривиальный делитель n.
±y(mod n). Тогда n\(x2—y2), но n не делит ни (x+y), ни (x—y), а значит НОД(x—y,n) – нетривиальный делитель n.
Методы случайных квадратов ищут случайным образом числа x, y: x2≡y2(mod n), а затем проверяют, что x 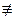 ±y(mod n).
±y(mod n).
Замечание: Если x, y – случайные числа, такие что x2≡y2(mod n), то P(x 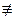 ±y(mod n)) ≤ 1/2. Действительно, сравнение a≡x2(mod n) имеет 2k различных корней, если n имеет k различных простых делителей, 2k—2 из которых подходят к вероятности.
±y(mod n)) ≤ 1/2. Действительно, сравнение a≡x2(mod n) имеет 2k различных корней, если n имеет k различных простых делителей, 2k—2 из которых подходят к вероятности.
Общий подход к поиску чисел x, y таков: выбирается факторная база S={p1, p2, … , pt}. Как правило, это t первых простых чисел.
Случайно выбирается несколько чисел ai, вычисляются числа bi=ai2 mod n и разлагается по факторной базе bi= 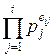 . Те числа bi, которые разложить по базе S не удалось, из дальнейшего рассмотрения исключаются. Всего требуется t+1 пара (ai, bi).
. Те числа bi, которые разложить по базе S не удалось, из дальнейшего рассмотрения исключаются. Всего требуется t+1 пара (ai, bi).
Затем из чисел bi составляется такое произведение B= 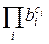 , ci
, ci 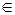 {0,1}, что B оказывается полным квадратом (то есть
{0,1}, что B оказывается полным квадратом (то есть 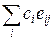 mod 2=0 для всех j). Вектор c находится путем решения соответствующей системы сравнений. Тогда
mod 2=0 для всех j). Вектор c находится путем решения соответствующей системы сравнений. Тогда
x= 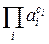 , y=
, y= 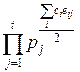 .
.
Очевидно, данная пара удовлетворяет сравнению x2≡y2(mod n). Если она удовлетворяет еще и условию x 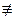 ±y(mod n), то НОД(x—y,n) есть нетривиальный делитель n. Иначе следует повторить данный метод, выбрав другие пары (ai, bi).
±y(mod n), то НОД(x—y,n) есть нетривиальный делитель n. Иначе следует повторить данный метод, выбрав другие пары (ai, bi).
Дата добавления: 2018-11-26; просмотров: 1260;











