Упражнения к Главе 2.
2.1. Вычислить сумму и произведение многочленов f(x) и g(x) на Z2[x]:
a) f(x)=x7+x5+x+1, g(x)=x4+x+1; c) f(x)=x8+x2, g(x)=x3+x2+1;
b) f(x)=x4+x, g(x)=x2+1; d) f(x)=x5; g(x)=x5+x.
2.2. Вычислить остаток от деления f(x) на g(x) на Z2[x].
a) f(x)=x8+x4+x+1, g(x)=x3+x+1; c) f(x)=x10+x2+x+1, g(x)=x2+x+1;
b) f(x)=x4+x, g(x)=x2+x+1; d) f(x)=x5+x4+1; g(x)=x2+x.
2.3. Вычислить НОД(g(x),f(x)) на Z2[x].
a) f(x)=x6+x5+x3+x2+1, g(x)= x5+x4+x+1;
b) f(x)=x6+x4, g(x)=x4+1;
c) f(x)=x4+x3+x2+x, g(x)=x5+x3;
d) f(x)=x9+x8+x; g(x)=x7+x4+x3+1.
Упражнения к Главе 3:
3.1. Осуществить 2-факторизацию следующих чисел, используя метод Ферма и метод квадратичного решета с решетами по модулям 4, 5, 7. Сравнить количество итераций для этих двух методов.
a) 12317; c) 7081; e) 551; g) 1679; i) 6111; k) 1221;
b) 851; d) 18161; f) 481; h) 7313; j) 1197; l) 609.
3.2. Осуществить 2-факторизацию следующих чисел, используя ро-метод Полларда.
a) 1183; b) 1881; c) 2597; d) 1057; e) 5461; f) 299.
3.3. Осуществить факторизацию следующих чисел, используя p—1 –метод Полларда.
a) 133; b) 209; c) 161; d) 527; e) 1393; f) 3277.
3.4. Вычислить следующие дискретные логарифмы, пользуясь алгоритмом «шаг младенца – шаг великана».
a) log3 14 mod φ(31); b) log5 42 mod φ(47); c) log3 30 mod φ(89).
3.5. При помощи алгоритма исчисления порядка вычислить следующие дискретные логарифмы.
a) log3 57 mod φ(89); b) log3 61 mod φ(79); c) log3 279 mod φ(587).
Ответы к упражнениям.
Упражнения к Главе 1:
1.1. a) 13, b) 2, c) 35, d) 6, e) 71, f) 43, g) 48, h) 160, i) 154.
1.2. a) 22·3·41, b) 3·11·23·29, c) 35·31, d) 24·7·37, e) 72·53, f) 2·32·11·19·131, g)7·113·67 h) 53·31·109, i) 2·34·71.
1.3. a) 24552, b) 6300, c) 10368, d) 1050, e) 7623, f) 219, g) 25048, h) 31189, i)43120.
1.4. a) 72, b) 54, c) 96, d) 294, e) 2, f) 12, g) 48, h) 2880, i) 16.
1.5. a) верно, b) верно, c) неверно, d) неверно, e) верно, f) неверно, g) верно, h)неверно, i) неверно.
1.7. a) —3; 12, b) 4; 4, c)—1; 80, d) 2; 2, e)—7; 8, f) 8; 8, g) 20; 20, h)—1; 2, i)0;0.
1.8. a) 5, b) 6, c) 11, d) 9, e) 7, f) не существует, g) 10, h) 21, i) 8.
1.9. a) 23, b) 4, c) 5, d) 43, e) 4, f) 18, g) 3, h) 8, i) 221.
1.10. a) x≡5(mod 11), b) x≡12(mod 13), c) x≡13(mod 17), d) x≡6, 15, 20(mod 21), e) x≡21, 52(mod 62); f) решений нет; g) x≡8(mod 16), h) x≡2+5t(mod 125), где t= 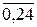 , i) x≡20(mod 29).
, i) x≡20(mod 29).
1.11. a) x≡8(mod 35), b) x≡52(mod 105), c) x≡53(mod 77), d) x≡101(mod 180), e) решений нет, f) x≡206(mod 210).
1.12. a) -1, b) -1, c) 1, d) 1, e) 0, f) 1, g) 1, h) 1, i) -1, j) -1, k) -1, l) -1.
1.13. a) ±6(mod 19), b) ±9(mod 13), c) ±7(mod 41), d) ±3(mod 7), e) ±5(mod 11), f) ±4(mod 11), g) решений нет, h) ±6(mod 17), i) ±6(mod 31).
1.14. a) ±4(mod 9), b) ±7(mod 25), c) ±9(mod 49), d) ±1(mod 4), e) решений нет, f) ±3, ±5(mod 16), g) ±1, ±15(mod 32), h) ±38(mod 81), i) ±53(mod 125), j) ±2(mod 6), k) ±1,±4(mod 15), l) ±1,±5,±7,±11(mod 24), m) ±9,±16(mod 35), n) решений нет, o) ±3,±7(mod 20), p) решений нет, q) ±2,±23,±37,±47(mod 105), r) ±4,±29 (mod 75).
1.15. a) решений нет, b) 2, c) 4, d) 4, e) 8, f) решений нет, g) 4, h) 2, i) 1.
1.18. 1011011101.
1.19. a) не существует, b) 24 корня, c) 24 корня, d) 40 корней, e) нет существует, f) 8 корней.
1.20. a) 3, b) 2, c) 2, d) 2, e) 17, f) 11, g) 3, h) 3, i) 2, j) 3, k) 3, l) 6.
Упражнения к Главе 2:
2.1. a) x7+x5+x4; x11+x9+x8+x7+x4+x2+1; b) x4+x2+x+1; x6+x4+x3+x; c) x8+x3+1; x11+x10+x8+x5+x4+x2; d) x; x10+x6.
2.2. a) x2+x+1, b) 0, c) x, d) 1.
2.3. a) (x+1), b) x2+1, c) x3+x, d) x2+x+1.
Упражнения к Главе 3:
3.4. a) 18, b) 24, c) 87.
3.5. a) 36, b) 45, c) 15.
Приложение 1.
Таблица простых чисел < 2558 и их наименьших первообразных корней.
| p | g | p | g | p | g | p | g | p | g | p | g | p | g | p | g |
| p | g | p | g | p | g | p | g | p | g | p | g | p | g |
Приложение 2.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
| . |
| ТЕОРЕТИКО - ЧИСЛОВЫЕ МЕТОДЫ В КРИПТОГРАФИИ |
| Рабочая программа для специальности |
| 075200 – Компьютерная безопасность |
Тюмень 2007
Дата добавления: 2018-11-26; просмотров: 965;











