Алгоритм Полига-Хеллмана.
Этот алгоритм использует следующий подход: пусть G – группа порядка n, и n= 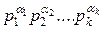 - каноническое разложение на простые сомножители. Если x=logga mod n, то, вычислив xi=logga mod
- каноническое разложение на простые сомножители. Если x=logga mod n, то, вычислив xi=logga mod 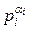 , для 1 ≤ i ≤ k, можно восстановить x, используя китайскую теорему об остатках.
, для 1 ≤ i ≤ k, можно восстановить x, используя китайскую теорему об остатках.
Для того чтобы вычислить xi, вычисляют коэффициенты l0, l1,…, 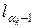 в pi-чном представлении числа xi: xi=l0+l1pi+…+
в pi-чном представлении числа xi: xi=l0+l1pi+…+ 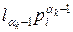 , где 0 ≤ lj ≤ pi—1.
, где 0 ≤ lj ≤ pi—1.
Представим метол Полига-Хеллмана следующим алгоритмом:
Алгоритм Полига-Хеллмана:
Вход: g – порождающий элемент циклической группы порядка n, a 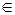 G.
G.
Ш.1. Найти каноническое разложение n= 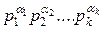 .
.
Ш.2. Для i от 1 до k выполнить следующие действия:
1. Задать q=pi, α=αi.
2. Задать γ=1, l-1=0.
3. Вычислить 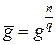 .
.
4. Для j от 1 до α—1 выполнить:
4.1. Вычислить γ=γ 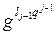 ,
, 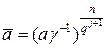
4.2. Вычислить li= 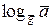 . (например, используя алгоритм «шаг младенца - шаг великана» или прямой поиск).
. (например, используя алгоритм «шаг младенца - шаг великана» или прямой поиск).
5. Вычислить xi=l0+l1q+…+lα—1qα—1.
Ш.3. Используя Китайскую теорему об остатках, решить систему сравнений x≡xi(mod 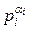 ) .
) .
Выход. x=logga mod n.
Замечание. Все вычисления производятся в группе G кроме случаев, когда оговорено иное.
Замечание. Поскольку порядок элемента 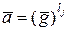 (в чем нетрудно убедиться, подставив вместо
(в чем нетрудно убедиться, подставив вместо 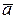 его выражение из 4.2 и учитывая, что порядок
его выражение из 4.2 и учитывая, что порядок 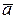 есть q), то li=
есть q), то li= 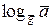 .
.
Заметим, что вычисление логарифма прямым поиском на этапе 4.2. происходит сравнительно быстро, так как приходится перебирать не более q значений.
Данный метод эффективен в случаях, когда n является большим числом, а все его простые сомножители – малыми числами.
Сложность данного алгоритма составляет O( 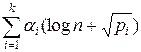 ) умножений в группе при условии, что разложение n известно.
) умножений в группе при условии, что разложение n известно.
Пример.
Пусть G=Z*p, p=61, g=2, a=7.
Ш.1. n=φ(p)=p—1=60=22·3·5.
Ш.2.
1. q=2, α=2.
2. γ=1, l-1=0.
3. 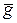 =230 mod 61=60.
=230 mod 61=60.
4. j=0  γ=1,
γ=1, 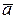 =730 mod 61 = 60
=730 mod 61 = 60  l0=log6060 mod 61=1.
l0=log6060 mod 61=1.
j=1  γ=2,
γ=2, 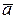 =(7·2-1)30mod 61=(7·31)30mod 61=1
=(7·2-1)30mod 61=(7·31)30mod 61=1  l0=log601 mod 61=0.
l0=log601 mod 61=0.
5. x1=1+0·2=1.
1. q=3, α=1.
2. γ=1, l-1=0.
3. 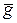 =220 mod 61=47.
=220 mod 61=47.
4. j=0  γ=1,
γ=1, 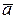 =720 mod 61 = 47
=720 mod 61 = 47  l0=log4747 mod 61=1.
l0=log4747 mod 61=1.
5. x2=1.
1. q=5, α=1.
2. γ=1, l-1=0.
3. 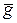 =212 mod 61=9.
=212 mod 61=9.
4. j=0  γ=1,
γ=1, 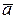 =712 mod 61 = 34
=712 mod 61 = 34  l0=log934 mod 61=4 (этот логарифм нашли прямым перебором).
l0=log934 mod 61=4 (этот логарифм нашли прямым перебором).
5. x3=4.
Ш.3. Составим и решим систему 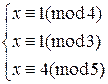 . Решением этой системы будет x≡48 (mod 60).
. Решением этой системы будет x≡48 (mod 60).
Проверка: 248mod 61=7.
Ответ: log27 mod 60 = 48.
Дата добавления: 2018-11-26; просмотров: 1212;











