Градиентные методы. Выбор шага

Будем рассматривать задачу:

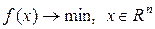(1)Пусть задано начальное приближение 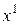. Основная идея, которая используется при разработке методов оптимизации – идея аппроксимации элементов задачи некоторыми более простыми элементами, в результате получается другая задача, которая является, как правило, задачей линейного программирования и решение этой задачи принимается за приближённое решение задачи (1).

Определение. Аппроксимацией 1-го порядка или линейной аппроксимацией функции 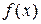класса 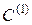в окрестности некоторой точки 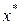называют линейную функцию

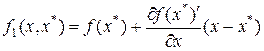(2)

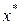Для в малой окрестности величина ~ .

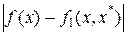Определение.Аппроксимацией 2-го порядка или квадратной аппроксимацией функции 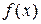класса 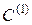в окрестности некоторой точки 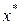называют функцию

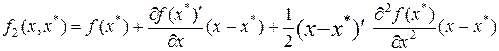(3)функция будет квадратичной функцией по и справедлива оценка ~ .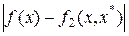

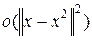Эти аппроксимации основаны на разложении в ряд Тейлора функции 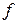. В оптимизации могут использоваться и другие виды аппроксимаций: если 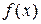– периодическая функция или близка к ней, то её можно аппроксимировать кусками рядов Фурье.