Теорема (Критерий Эйлера)
Если (p, a)=1 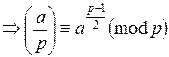
Доказательство:
По теореме Ферма, ap--1≡1(mod p). В этом сравнении перенесем единицу в левую часть: ap—1—1≡0(mod p). Поскольку p – простое, а значит нечетное число, значит p—1 – число четное. Тогда можем разложить левую часть сравнения на множители: 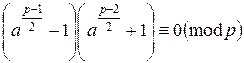 .
.
Из множителей в левой части один и только один делится на p, то есть либо
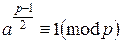 *, либо
*, либо 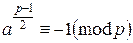 **
**
Если а – квадратичный вычет по модулю р, то а при некотором x удовлетворяет сравнению a≡x2(mod p) , тогда 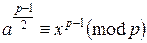 , а учитывая (по теореме Ферма), что xp—1≡1(mod p), получаем сравнение (*).
, а учитывая (по теореме Ферма), что xp—1≡1(mod p), получаем сравнение (*).
При этом решения сравнения * исчерпываются квадратичными вычетами по модулю р. Следовательно, если а – квадратичный невычет по модулю р, то сравнение * не выполняется, а значит выполняется сравнение **.
□
Свойство 2:
Доказательство следует из того, что все числа одного класса вычетов по модулю р будут одновременно квадратичными вычетами или квадратичными невычетами.
□
Свойство 3:
Для любого p выполняется 1≡12(mod p), а значит «1» является квадратичным вычетом для любого модуля p.
□
Свойство 4:
Доказательство следует из критерия Эйлера при a=—1.
□
Свойство 5:
По критерию Эйлера, 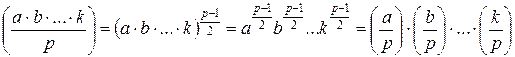 .
.
□
Доказательства прочих свойств можно произвести самостоятельно или найти в [5].
Итак, символ Лежандра можно найти, пользуясь либо критерием Эйлера, либо используя свойства 2-8:
Пример:
a) 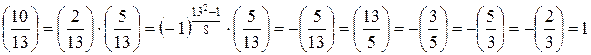
10 – квадратичный вычет по модулю 13.
б) 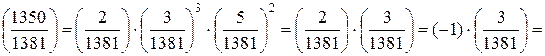
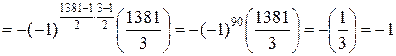 .
.
1350 не является квадратичным вычетом по модулю 1381.
Пусть n – составное число, каноническое разложение которого есть 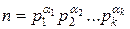 . Положим (a,n)=1. Тогда символ Якоби определяется равенством:
. Положим (a,n)=1. Тогда символ Якоби определяется равенством: 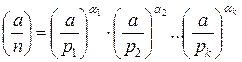
Свойства символа Якоби:
1. a≡a1(mod n) 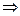
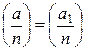
2. 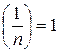
3. 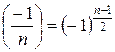
4. 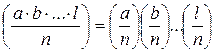
5. 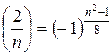
6. 3акон взаимности:
(n,m)=1, n, m>0, n, m — нечетные числа 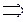
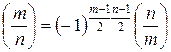 .
.
Эти свойства нетрудно доказать, воспользовавшись определением символа Якоби и свойствами символа Лежандра.
Очевидно, для символа Якоби выполняются те же свойства, что и для символа Лежандра, за исключением только критерия Эйлера. Критерий Эйлера для символа Якоби не выполняется.
Приведенные свойства символа Якоби позволяют составить алгоритм для вычисления символа Якоби и символа Лежандра:
1. Выделяем из числителя все степени двойки:
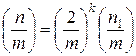
2. Пользуясь св-вом 4, понижаем степень k:
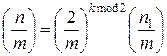
3. Если k mod 2=1, то вычисляем 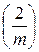 пользуясь св-вом 5.
пользуясь св-вом 5.
4. Символ 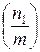 преобразуем, пользуясь законом взаимности, и затем приводим числитель m по модулю знаменателя n1 и повторяя для получившегося символа Якоби шаги 1-4, пока в числителе не останется 1 или —1.
преобразуем, пользуясь законом взаимности, и затем приводим числитель m по модулю знаменателя n1 и повторяя для получившегося символа Якоби шаги 1-4, пока в числителе не останется 1 или —1.
В более формализованном виде алгоритм выглядит следующим образом:
Алгоритм вычисления символа Якоби:
Вход: n - числитель, m – знаменатель символа Якоби. m – нечетное число,
n, m>0, s=1.
Ш.1: Если (n,m)≠1, то s:=0. Идти на Выход.
Ш.2: n:=n mod m. Ш.3.
Ш.3: Представить n как n=2kn1 . k:=k mod 2, n:=n1.
Ш.4: Если k=1, то если m mod 8 = 3 или m mod 8 = 5, то s:=—s .
Ш.5: Если n=1, то идти на Выход.
Ш.6: Если n=m—1, и m mod 4 = 1, то идти на Выход.
Если n=m—1, и m mod 4 = 3, то s:=—s. Идти на Выход.
Ш.7: n↔m. s:=s·(—1) 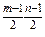 . Идти на Ш.2.
. Идти на Ш.2.
Выход. s – символ Якоби.
Пример:
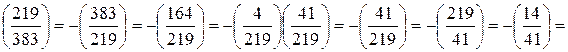
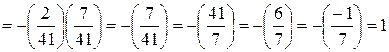 .
.
Дата добавления: 2018-11-26; просмотров: 1369;











