Сравнения любой степени по составному модулю.

Теорема

Если m₁, m₂, … , m_k – попарно простые числа, то сравнение

f(x)≡0(mod m₁·m₂·…·m_k) *

равносильно системе

** ,

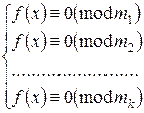причем, если первое сравнение имеет T₁ решений по модулю m₁, второе – T₂ решений модулю m₂, …, k-е сравнение имеет T_k решений по модулю m_k, то исходное сравнение будет иметь T=T₁·T₂·…·T_k решений по модулю m₁·m₂·…·m_k.

Доказательство:

Равносильность сравнения и системы очевидна и следует из свойств 12 и 13 сравнений.

Утверждение о количестве решений следует из того, что каждое сравнение

f(x)≡0(mod m_s) ***

выполняется тогда и только тогда, когда выполняется одно из T_s сравнений вида x≡b_s(mod m_s) (где b_s пробегает вычеты решений сравнения ***). Причем возможно всего T=T₁·T₂·…·T_k различных комбинаций вида x≡b₁(mod m₁), x≡b₂(mod m₂),…, x≡b_k(mod m_k), которые приводят (по китайской теореме об остатках) к различным классам вычетов по модулю m₁·m₂·…·m_k.

□

Из доказанной теоремы следует, что решение сравнения вида 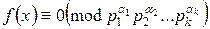сводится к решению сравнений вида .

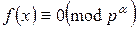А решение сравнение вида f(x)≡0(mod p^α) может быть найдено, если известно решение сравнения f(x)≡0(mod p). Покажем это.

Пусть x≡x₁(mod p) – решение сравнения f(x)≡0(mod p). Тогда x можно представить в виде

x=x₁+pt₁, где .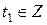

Подставляя такое x в сравнение f(x)≡0(mod p²) и применяя формулу Тейлора (учитывая, что f(x) – многочлен, x₁ – целое число, поэтому 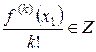), получаем

f(x₁)+pt₁f '(x₁)≡0(mod p²).

Поскольку f(x₁)≡0(mod p), то p\f(x₁), а значит можно сократить в получившемся выражении на p правую, левую части и модуль. Получим:

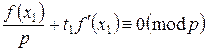
Если f '(x₁) не делится на р, то данное сравнение имеет одно решение:

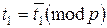(т.е. )

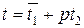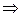
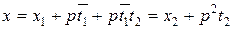
Подставляя полученное x в сравнение f(x)≡0(mod p³), имеем

f(x₂)+p²t₂f '(x₂)≡0(mod p³),

откуда, сократив правую, левую части и модуль на p² , получим

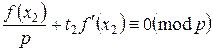
[Здесь f '(x₂) не может быть кратно р, если f '(x₁) не кратно p, т.к. x₂≡x₁(mod p), а значит, f '(x₂) ≡ f '(x₁) (mod p)]

Тогда сравнение имеет одно решение 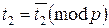, или, что то же самое, 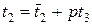, откуда получаем решение по модулю p³ : x=x₃+p³t₃.

Продолжим этот процесс до тех пор, пока не будет решено сравнение по модулю p^α. Итак, по данному решению сравнения f(x)≡0(mod p) можно найти решение сравнения f(x)≡0(mod p^α).

Пример:

Требуется решить сравнение x³+9x—1≡0 (mod 125).

Известно, что сравнение x³+9x—1≡0 (mod 5) имеет одно решение:

x≡2(mod 5), или x=2+5t₁.

Поскольку модуль «5» небольшой, а общих подходов к сравнениям высоких степеней мы пока не знаем, то этот корень нашли простым перебором, попутно убедившись в его единственности.

Подставим получившееся x в сравнение по модулю 25:

(2+5t₁)³+9(2+5t₁)—1≡0 (mod 25).

Решим это сравнение.

8+4·5t₁+2·(5t₁)²+(5t₁)³+18+9·5t₁—1≡0 (mod 25)

25+13·5t₁+25·(5t₁³+2 t₁²) ≡0 (mod 25)

13·5t₁≡0 (mod 25)

13t₁≡0 (mod 5)

t₁≡0 (mod 5)

Или, что то же самое, t₁=0+5t₂, откуда решение по модулю 25 есть x=2+25t₂. Подставим полученное x в сравнение по модулю 125:

(2+25t₂)³+9(2+25t₂)—1≡0 (mod 125)

Решим это сравнение.

8+4·25t₂+2·(25t₂)²+(25t₁)³+18+9·25t₁—1≡0 (mod 125)

25+13·25t₂+625·(25t₂³+2t₂²) ≡0 (mod 125)

25+13·25t₂≡0 (mod 125)

1+13t₂≡0 (mod 5)

13t₂≡—1 (mod 5)

3t₂≡4 (mod 5)

Получили сравнение первой степени. Решим его. Отыщем 3^-1(mod 5), для чего, как всегда, воспользуемся расширенным алгоритмом Евклида:

5=3+2

3=2+1

2=1+0

1=3—2=3—(5—3)=2·3—1·5.

2≡3^-1(mod 5).

Тогда решением сравнения относительно t₂ будет

t₂≡2·4 (mod 5)

t₂≡3 (mod 5)

Или, что то же самое, t₂=3+5t₃, откуда решение по модулю 125 есть x=2+25(3+5t₃)=2+75+125t₃=77+125t₃, или, что то же самое,

x≡77 (mod 125).