Сравнения любой степени по простому модулю.
Пусть р – простое число, и пусть задано сравнение вида f(x)≡0(mod p), где f(x)=axn+a1xn—1+…+an *. Тогда справедлива
Теорема 1:
Сравнение вида * равносильно сравнению степени, не выше р—1.
Доказательство:
Деля f(x) на (xp—x) с остатком, имеем f(x) =(xp—x)Q(x)+R(x).
Так как xp—x≡0(mod p), то f(x)≡R(x)(mod p), а степень многочлена R(x) не выше, чем р–1. Что и требовалось доказать.
□
Теорема 2
Если сравнение * имеет более n решений, то все коэффициенты многочлена f(x) кратны р.
Доказательство:
Пусть * имеет хотя бы n+1 решение, и вычеты этих решений суть x1, x2, … , xn, xn+1.
Тогда многочлен f(x) можно представить в виде
f(x)=a(x—x1)(x—x2)(x—x3)…(x—xn)+ **
+b(x—x1)(x—x2)…(x—xn—1)+
+c(x—x1)(x—x2)…(x—xn—2)+
……...
+l(x—x1)+m.
Справедливость этого равенства проверяется раскрытием скобок в правой части.
Полагая в этом равенстве x=x1, убеждаемся, что p\m, полагая x=x2 и учитывая, что p\m, убеждаемся, что р\l. Полагаем, что x=x3, x=x4, …, x=xn+1 и последовательно убеждаемся, что p\c, p\b, p\a, то есть все коэффициенты из ** делятся на p.
Учтем, что a=a, 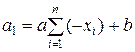 ,
, 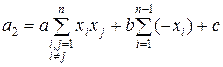 , … ,
, … , 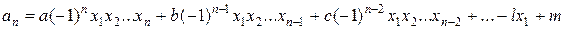 , то есть коэффициенты из * являются линейными комбинациями коэффициентов из **, а значит a, a1, a2, …, an кратны р как линейные комбинации чисел, кратных р.
, то есть коэффициенты из * являются линейными комбинациями коэффициентов из **, а значит a, a1, a2, …, an кратны р как линейные комбинации чисел, кратных р.
□
Дата добавления: 2018-11-26; просмотров: 969;











