Применения китайской теоремы об остатках.
Китайская теорема об остатках находит широкое применение в теории чисел и криптографии.
Применение Китайской теоремы об остатках в криптосистеме RSA.
В криптосистеме RSA при расшифровании требуется вычислить ydmod n, причем известно, что n=p∙q, где p, q – большие простые числа. Как было показано ранее, степень d, в которую требуется возвести шифрованный текст, можно понизить за счет использования теоремы Эйлера. Зная разложение числа n на простые сомножители и используя китайскую теорему об остатках, возможно еще более ускорить вычисления.
Сначала вычисляют:
r1=yd mod p=(y mod p)d mod (p–1)mod p,
r2=yd mod q=(y mod q)d mod (q–1)mod q.
Как читатель мог заметить, при вычислениях для ускорения возведения в степень используется теорема Ферма.
Получим систему сравнений
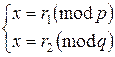 .
.
Решая ее по китайской теореме об остатках, получим решение 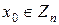 .
.
Сложность возведения в степень с использованием китайской теоремы об остатках и теоремы Ферма составляет около 6k3 против 24k3 при использовании только теоремы Ферма (где k есть размерность числа n).
Пример.
Пусть в RSA 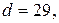
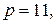
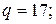
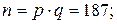
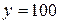
Требуется вычислить x=10029 mod 187.
Вычисляем:
r1=(100 mod 11)29 mod 10 mod 11=19 mod 11 = 1,
r2=(100 mod 17)29 mod 16 mod 17=1513 mod 17=2.
Cоставляем систему
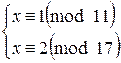
Пользуясь Китайской теоремой об остатках, решаем эту систему.
| mi | ||
| Mi | ||
| M’i |
Получаем
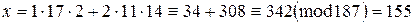
Ответ: 10029 mod 187=155.
Схема разделения секрета на основе Китайской теоремы об остатках.
На основе китайской теоремы об остатках можно построить (n,k)–пороговую схему разделения секрета. Напомним основные принципы схем разделения секрета.
Пусть существует некая информация, которую следует сохранить в секрете, и имеется n участников, не доверяющих друг другу. Эти участники хотят, чтобы секретную информацию можно было получить только при условии того, что как минимум k участников из n собрались вместе.
(n,k)-пороговая схема разделения секрета – это схема разделения секретной информации между n участниками таким образом, чтобы только k из них (или более), собравшись вместе, могли получить этот секрет. Причем вероятность угадать верное значение секрета при наличии k–m долей секрета 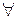 m>0 равна вероятности угадать верное значение секрета без обладания долей секрета. При этом все участники протокола равноправны.
m>0 равна вероятности угадать верное значение секрета без обладания долей секрета. При этом все участники протокола равноправны.
Как правило, схемы разделения секрета состоят из 2-х фаз: фазы разделения, когда каждому участнику протокола выдается его доля секрета, и фаза восстановления, когда k или более любых участников, собрав свои доли, восстанавливают общий секрет.
Схема разделения секрета на основе китайской теоремы об остатках выглядит следующим образом:
Пусть N – общий секрет.
Разделение секрета:
Берем p1, p2,…, pn – различные простые числа.
Часть секрета, выдаваемая i-му участнику схемы, есть число xi, вычисляемое как xi≡N(mod pi).
Заметим, что числа p1, p2,…, pn должны быть такими, чтобы произведение любых k из них было больше, чем N. А это достигается, когда для всех i выполняется pi> 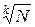 .
.
Для того, чтобы k–1 участников не смогли восстановить секрет без k-го участника, необходимо, чтобы pi << 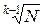 .
.
Итак, относительно чисел p1, p2,…, pn должны выполняться условия:
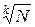 < pi <<
< pi << 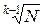
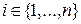 .
.
Восстановление секрета:
Собравшись вместе, k участников составляют и решают систему сравнений 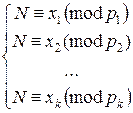 .
.
Решив систему, участники получают общий секрет N.
Дата добавления: 2018-11-26; просмотров: 1161;











