Тест на простоту Соловея-Штрассена.
Символ Якоби отличается от символа Лежандра тем, что в первом знаменатель – составное число, а во втором – простое. Алгоритм вычисления символа Якоби и символа Лежандра одинаков, но для символа Якоби не выполняется критерий Эйлера.
Пусть мы имеем нечетное число n, о котором неизвестно, простое оно или составное. Символ 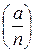 является символом Лежандра, если n – простое, и тогда для него выполняется критерий Эйлера, то есть
является символом Лежандра, если n – простое, и тогда для него выполняется критерий Эйлера, то есть 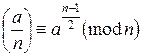 .
.
Если же n – составное число, то символ 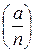 является символом Якоби, и тогда вышеуказанное сравнение, возможно, не выполняется. (Мы говорим «возможно», так как для некоторых a и n, в силу случайного совпадения, сравнение может оказаться верным.)
является символом Якоби, и тогда вышеуказанное сравнение, возможно, не выполняется. (Мы говорим «возможно», так как для некоторых a и n, в силу случайного совпадения, сравнение может оказаться верным.)
Поэтому если найдется такое a (1 < a < n), что 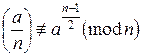 , то можно наверняка утверждать, что число n – составное. На этом факте основан тест Соловея-Штрассена.
, то можно наверняка утверждать, что число n – составное. На этом факте основан тест Соловея-Штрассена.
Тест Соловея-Штрассена:
Вход: n – нечетное, t – параметр надежности.
1. Повторять t раз:
1.1 Случайно выбираем a: 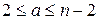
1.2. Если 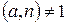
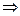 “n – составное”. Выход.
“n – составное”. Выход.
1.3. Вычисляем 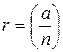 ,
, 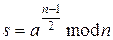
1.4. Если r ≠s 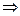 “n –составное ”. Выход.
“n –составное ”. Выход.
2. “n –простое с вероятностью 1— εt ”. Выход.
Как и тест Ферма, этот тест может принять составное число за простое, но не наоборот. Вероятность ошибки (то есть вероятность принять составное число за простое) составляет εt, где t – число итераций теста, параметр надежности, а 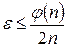 <
< 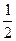 .
.
Как видим, оценка надежности теста Соловея–Штрассена гораздо лучше, чем для теста Ферма, даже в том случае, когда φ(n) ненамного меньше n.
Дата добавления: 2018-11-26; просмотров: 1313;











