Теорема (о делителях числа)

Пусть 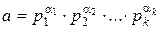– каноническое разложение числа a. Тогда все делители а имеют вид

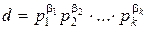, где 0≤β₁≤α₁, 0≤β₂≤α₂, …, 0≤β_k≤α_k.

Доказательство:

Пусть q\a a представимо в виде a=dq, тогда все простые делители числа d входят в каноническое разложение числа а с показателями, не меньшими тех, с которыми они входят в каноническое разложение числа а.

□

Следствие 1

Количество различных делителей числа 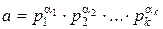есть .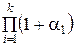

Доказательство очевидно, оно следует из числа всевозможных сочетаний в формуле делителя в теореме о делителях числа.

Следствие 2

НОД(a₁,…,a_n), где 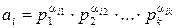( 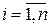), есть 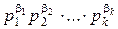, где ( ).

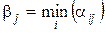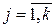Пример.

a₁=2∙3∙5²=150, a₂=2²∙5∙7=140, a₃=2³∙5=40.

p₁=2, p₂=3, p₃=5, p₄=7.

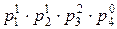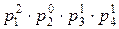a₁= , a₂= , a₃= .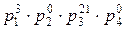

НОД(a₁,a₂,a₃)= 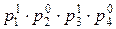=2∙5=10.

Следствие 3

Совокупность общих делителей a₁,…,a_n совпадает с совокупностью делителей НОД(a₁,…,a_n).

Следствие 4

НОК 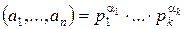, где ,

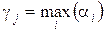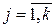
Пример.

НОК(150,140,40)=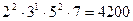

Следствие 5

Если a₁,…,a_n – попарно простые числа, то НОК(a₁,…,a_n)= a₁∙…∙a_n

Следствие 6

Совокупность общих кратных чисел a₁,…,a_n совпадает с совокупностью кратных их наименьшего общего кратного.

Доказательства следствий 1–6 предоставляется читателю в качестве упражнения. Отыскать эти доказательства можно в [5] (Виноградов, «Основы теории чисел»).