Мультипликативные функции.
Введем функции 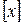 – целая часть от x ,
– целая часть от x , 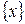 – дробная часть от x.
– дробная часть от x.
Функция Θ(a) называется мультипликативной, если:
1. Определена для 
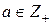 , и при этом
, и при этом 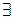 a1:Θ(a1)≠0;
a1:Θ(a1)≠0;
2. 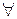
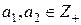 : (a1,a2)=1
: (a1,a2)=1  Θ(a1∙a2)=Θ(a1)∙Θ(a2).
Θ(a1∙a2)=Θ(a1)∙Θ(a2).
Пример:
Степенная функция 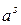 – мультипликативная функция.
– мультипликативная функция.
Свойства мультипликативных функций:
1. Если Θ(a) – мультипликативная функция, то Θ(1)=1.
Доказательство:
По определению мультипликативной функции, найдется a1: Θ(a1)≠0.
Тогда Θ(a1)=Θ(a1∙1)=Θ(a1) ∙ Θ(1). Отсюда Θ(1)=1.
□
2. Если Θ – мультипликативная функция, то для попарно простых чисел a1,a2,…,ak выполняется Θ(a1∙a2∙…∙ak)= Θ(a1)∙Θ(a2)∙…∙Θ(ak).
В частности, 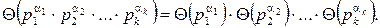
(Доказательство очевидным образом следует из 2-го условия на мультипликативную функцию.)
3. Если функции Θ1, Θ2, … ,Θk – мультипликативные, то их произведение Θ=Θ1∙Θ2∙…∙Θk – также мультипликативная функция.
4. Если Θ(a) – мультипликативная функция, 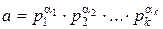 – каноническое разложение а, то, обозначив знаком
– каноническое разложение а, то, обозначив знаком 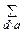 сумму по всем делителям числа а, имеем
сумму по всем делителям числа а, имеем
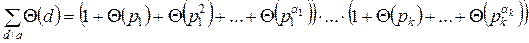
(Доказываем, раскрывая скобки в правой части).
Функция Эйлера.
Функция Эйлера φ(a) есть количество чисел ряда 0, 1, …, а–1, взаимно простых с а ( 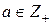 ).
).
φ(1)=1, φ(2)=1, φ(3)=2, φ(4)=2, φ(5)=4, φ(6)=2 и т. д.
Свойства функции Эйлера:
1) φ(1)=1;
Доказательство следует из определения.
2) φ(p)=p–1, где р – простое;
Доказательство:
Действительно если р – простое, в ряду чисел 0, 1, …, p–1 не является взаимно простым с p только «0». Остальные p–1 чисел являются взаимно простыми с p в силу его простоты. Воспользовавшись определением функции Эйлера, получим искомое.
□
3)φ(pα)=pα–1(p–1) , где р – простое;
Доказательство:
Рассмотрим ряд чисел 0, 1, … , p, … , 2p, … , 3p, … , p2, … ,(p+1)p, … ,pα--1.
В этом ряду не взаимно простыми с pα являются только те числа, которые кратны p, то есть числа 0, p, 2p, …, (pα–1–1)p. Таких чисел будет pα–1. Всего же чисел в этом ряду будет pα.
Таким образом, количество чисел в рассматриваемом ряду, взаимно простых с pα будет pα–pα–1= pα–1(p–1). Итак, φ(pα)=pα–1(p–1).
□
4)φ(a) – мультипликативная функция.
Доказательство:
Действительно, по определению функции Эйлера, она задана для всех положительных чисел, и согласно свойству №1 функции Эйлера, φ(1)=1.
Покажем, что φ(p1p2)=φ(p1)φ(p2), если p1, p2 – простые числа.
Действительно, в ряду чисел 0, 1, … , p1p2—1 ровно p2 чисел являются кратными p1 и ровно p1 чисел будут кратны p2. Причем, в силу взаимной простоты p1 и p2, это будут разные числа, и только число «0» кратно и p1, и p2. Таким образом, чисел, кратных p1 или p2 будет p1+p2—1. Тогда чисел, взаимно простых и с p1, и с p2 будет ровно p1p2—p1—p2+1=p1(p2—1)—(p 2—1) =(p1—1)(p2—1)= φ(p1)φ(p2).
Покажем теперь, что для взаимно простых чисел a1 и a2 справедливо φ(a1a2)=φ(a1)φ(a2).
Действительно, в ряду чисел 0, 1, … , a1a2—1 ровно a1a2—φ(a1)a2 чисел будут не взаимно простыми с a1 и a1a2—φ(a2)a1 чисел – не взаимно простыми с a2.
В то же время в ряду чисел 0, 1, … , a1—1 ровно a1— φ(a1) чисел не будут являться взаимно простыми с a1, в ряду чисел 0, 1, … , a2—1 ровно a2— φ(a2) чисел не будут являться взаимно простыми с a2. То есть среди чисел 0, 1, … , a1a2—1 не взаимно простыми одновременно и с a1 , и с a2 будут являться (a1—φ(a1))(a2—φ(a2)) чисел.
Таким образом, общее количество взаимно простых с a1a2 среди натуральных чисел, меньших a1a2, есть
a1a2—( a1a2—φ(a1)a2+ a1a2—φ(a2)a1—(a1—φ(a1))(a2—φ(a2)))=
= a1a2— (a1a2—φ(a1)a2— φ(a2)a1+ φ(a1)a2+ φ(a2)a1— φ(a1)φ(a2))= φ(a1)φ(a2).
Итак, доказали, что функция Эйлера – мультипликативная.
Пример
Вычислим φ(28350322).
Для того, чтобы вычислить значение функции Эйлера, необходимо найти каноническое разложение аргумента.
28350322=2·14175161=2·7·2025023=2·72·289289=2·73·41327=
=2·73·11·3757=2·73·11·13·289=2·73·11·13·172.
φ(28350322)= φ(2·73·11·13·172)= φ(2) · φ(73)· φ(11)· φ(13)· φ(172)=
=1·72·6·10·12·17·16=9596160.
Ответ: φ(28 350 322)=9 596 160.
Теория сравнений
Будем рассматривать целые числа в связи с остатками от деления их на данное целое положительное m – модуль. Если 2 целых числа a и b имеют одинаковый остаток от деления на m, то говорят, что они называются равноостаточными или сравнимыми по модулю m, и пишут a ≡ b (mod m), что равносильно a = b+mt, где t 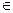 Z, или m\(a–b) (очевидно)
Z, или m\(a–b) (очевидно)
3.1. Свойства сравнений:
1. a ≡ b (mod m), b ≡ c (mod m),  a ≡ c (mod m)
a ≡ c (mod m)
2. a ≡ b (mod m) 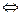 b ≡ a (mod m)
b ≡ a (mod m)
3. a1 ≡ b1 (mod m), a2 ≡ b2 (mod m), … , ak ≡ bk (mod m) =>
a1+…+ak ≡ b1+…bk(mod m)
4. a+b ≡ c (mod m)  a ≡ c–b (mod m)
a ≡ c–b (mod m)
5. a ≡ b (mod m)  a+mt ≡ b+mk(mod m) (t, k
a+mt ≡ b+mk(mod m) (t, k 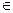 Z)
Z)
6. a ≡ b (mod m), c ≡ d (mod m)  ac ≡ bd (mod m)
ac ≡ bd (mod m)
7. a ≡ b (mod m)  ak ≡ bk(mod m)
ak ≡ bk(mod m)
8. a ≡ b (mod m)  ak ≡ bk(mod m)
ak ≡ bk(mod m)
9. Если a ≡ b (mod m), (a, b) = c, (c, m) = 1 
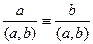 (mod m)
(mod m)
10. a ≡ b (mod m)  ak ≡ bk (mod mk)
ak ≡ bk (mod mk)
11. a ≡ b (mod m), a = a1d, b = b1d, m = m1d  a1 ≡ b1(mod m1)
a1 ≡ b1(mod m1)
12. a ≡ b (mod m1), a ≡ b(mod m2), …, a ≡ b(mod mk) 
a ≡ b (mod НОК(m1,…,mk))
13. a ≡ b (mod m), d\m  a ≡ b(mod d)
a ≡ b(mod d)
14. d\a, d\m, a ≡ b(mod m)  d\b
d\b
15. a ≡ b (mod m)  (a, m) = (b, m)
(a, m) = (b, m)
Доказательство данных свойств не представляет сложности и может быть проведено читателем самостоятельно. Найти доказательства этих свойств можно в [5].
Дата добавления: 2018-11-26; просмотров: 1134;











