Асимптотический закон распределения простых чисел.

Решето Эратосфена отыскивает все простые числа от 1 до N. Однако при большом N поиск простых чисел таким способом отнимает много времени. Современная практическая криптография требует использования больших простых чисел – в некоторых стандартах используются простые числа размером порядка 1024 бита.

По понятным причинам, невозможно организовать поиск таких больших простых чисел при помощи решета Эратосфена. В настоящее время разработано несколько вероятностных и детерминированных тестов на простоту. Эти тесты определяют, является ли наугад выбранное число простым или составным. Далее мы изучим такие вероятностные тесты, как тест Ферма, Соловея-Штрассена, Миллера-Рабина.

Для поиска простых чисел с помощью таких тестов используют следующий подход: из чисел заданного диапазона случайным образом выбирают числа и проверяют их на простоту. Поиск прекращается как только будет найдено простое число. Такой подход называют случайным поиском простых чисел.

Для того чтобы оценить время, которое придется затратить на случайный поиск в заданном диапазоне, необходимо знать, сколько примерно простых чисел в этом диапазоне содержится. Конечно, точное распределение простых чисел в N неизвестно, но некоторые сведения об этом распределении у современной математики имеются. Так, в п.4 мы привели теоремы Евклида о простых числах, в которых утверждается, что, с одной стороны, простых чисел бесконечно много, а значит найдется сколь угодно большое простое число, а с другой стороны – что для любого m найдутся m подряд идущих составных, то есть существуют такие сколь угодно длинные диапазоны, на которых простых чисел нет вообще.

Более точно на вопрос о распределении простых чисел в N отвечает асимптотический закон распределения простых чисел.

Итак, обозначим π(x) – количество простых чисел, меньших либо равных x. Тогда справедлив

Асимптотический закон простых чисел

.

■

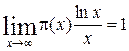Другими словами, при x→∞, π(x)→x/lnx.

Кроме того, справедлива