Теорема Чебышева (1850 г.)

Для любого x при некоторых c₁<1< c₂ выполняется .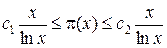

■

Учитывая асимптотический закон, можно сказать, что чем x больше, тем c₁ и с₂ ближе к 1.

Для x>1 с₂<1,25506, для x≥17 с₁=1.

Пример.

Пользуясь асимптотическим законом, вычислим примерное количество простых 512-битных чисел (таких, чтобы старший, 512-й, бит был равен 1).

Наименьшее значение 512-битного числа составляет 2⁵¹¹, наибольшее – 2⁵¹²-1.

Таким образом, нужно найти приблизительное количество K простых чисел из диапазона (x₁=2⁵¹¹, x₂=2⁵¹²).

K = π(x₂)—π(x₁) ≈ = = = = = .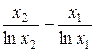

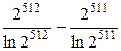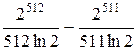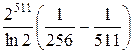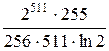Тогда вероятность при случайном поиске в заданном диапазоне выбрать простое число составляет

P = ≈ = ≈ .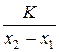

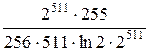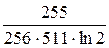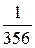Если же случайный поиск производить только среди нечетных чисел, то

P = ≈ .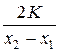

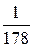То есть для того, чтобы путем случайного перебора среди 512-битных нечетных чисел найти простое, в среднем понадобится 178 итераций.

Для 1024-битных чисел поиск среди нечетных чисел потребует в среднем 355 итераций.

В общем, при увеличении требуемого размера числа (в битах) в 2 раза, среднее время поиска тоже увеличивается в два раза.

Функция Эйлера.