Теорема Евклида (о простых числах) №1

Простых чисел бесконечно много.

Доказательство:

Пусть простых чисел ровно k штук, и p₁,…,p_k – все простые числа.

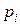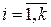
Возьмем n=p₁∙p₂∙…∙p_k+1. По предположению, n – составное число, т.к. n> , существует простое число d: d\n.

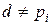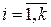
Но очевидно, исходя из вида числа n, что , получили противоречие с тем, что p₁,…,p_k – все простые числа.

□

Теорема Евклида (о простых числах) №2

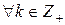в числовом ряду (1, 2, 3, …) существует k подряд идущих составных чисел.

Доказательство:

Возьмем m=k+1.

m!+2, m!+3,…, m!+m – составные числа, и их ровно k штук.

□

Решето Эратосфена

Решето Эратосфена используется для составления таблицы простых чисел, меньших или равных наперед заданного натурального числа N.

1. Выписываем числа 1 2 3 … N

2. Первое число, которое больше, чем 1, есть 2. Двойка делится только на 1 и 2, т.е. является простым числом.

Вычеркиваем из ряда (как составные) все числа, кратные 2, кроме самой двойки.

3. Второе невычеркнутое число есть 3. Оно не делится на 2, иначе оно оказалось бы вычеркнутым, значит 3 делится только на 1 и 3, значит 3 – простое число.

Вычеркиваем из ряда все числа, кратные 3.

4. Следующее невычеркнутое число есть 5. Оно простое, так как не делится ни на одно число, меньшее самого себя, иначе оно было бы вычеркнуто. Вычеркиваем все числа, кратные 5, кроме самой пятерки.

Этот процесс продолжаем далее для всех невычеркнутых чисел.

Когда этим способом вычеркнуты все числа, меньшие p (p – простое), то все невычеркнутые числа, меньшие p², будут простыми.

Действительно, всякое составное а<p² уже вычеркнуто, как кратное его наименьшего делителя d: a=da₁ который d≤ 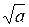<p (по утверждению 2).

Тогда следуют правила:

1. Числа, кратные р, вычеркиваются, начиная с p².

2. Составление таблицы простых чисел, меньших или равных N, закончено, как только вычеркнуты все кратные простых, меньших или равных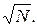

Пример: N=50 .

1 2 3 45 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50