Интервальные оценки (доверительные интервалы)

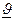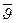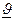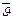Доверительным интервалом (ДИ) для параметра J, соответствующим доверительной вероятности g (обычно g = 0,95), называется интервал J_g(J) = ( , ), где и - нижняя и верхняя границы, которые определяются по выборочным данным так, чтобы 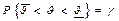, т.е. вероятность “накрытия” интервалом неизвестного значения параметра J равна доверительной вероятности (уровню доверия) g. Нижняя и верхняя границы доверительного интервала являются СВ так как определяются по результатам наблюдений. Полуширина доверительного интервала определяет точность оценки, а g = 1 - a - ее достоверность, a - уровень значимости.

Постановка задачи. Пусть СВ X ~ N(m, s). По выборке объема n требуется построить ДИ для параметров m и s с уровнем доверия g, т.е.:

J_g(m) = ( 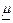, 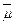) и J_g(s) = ( , ).

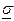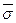ДоверительныЙ интервал J_g(m) = ( , )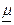

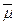Случай I (s = s₀ - известная величина). Будем искать симметричный ДИ в виде J_g(m) = ( 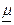, 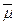) = ( 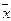-e, 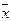+e), где 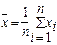- выборочное среднее параметра m. Тогда остается найти e > 0, соответствующее доверительной вероятности g, чтобы P{ 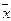-e < m < 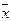+e} = g. Если X ~ N(m, s₀), тогда СВ 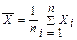~ N(m, s₀/ 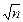). Следовательно 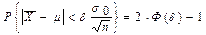. Тогда e = d×s₀/ 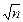и 2Ф(d) - 1 = g. Определим из этих двух уравнений d и e.

Очевидно, что d = t_(g+1)/2 - квантиль уровня (g+1)/2 нормального распределения, который находится по соответствующим таблицам.

Тогда e(g) = t_(g+1)/2×s₀/ 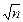. Тем самым получен ДИ для параметра m следующего вида:

J_g(m) = ( 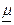, 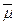) = ( 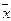-e, 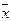+e), где 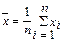и e = t_(g+1)/2×s₀/ .

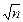Пример. Измеряется глубина проникания L с помощью прибора, которое имеет среднеквадратичное отклонение погрешности измерения s₀ = 10 мм. Проведено четыре измерения и определено выборочное среднее 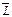= 152 мм. Считая, что L ~ N(m, s₀), определить доверительный интервал глубины L с уровнем доверия g = 0,9.

Решение. Сначала определим квантиль уровня 0,95 нормального распределения: t_(g+1)/2 = t_0,95 = 1,65.

Следовательно J_0,95(m) = ( 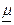, 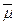) = ( 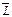- e, 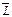+ e), где e = t_0,95×s₀/ 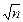= 1,65×10/2 = 8,25. Тогда J_0,95(m) = 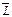± e = 152 ± 8,3 мм.

Задача 2. Как изменится доверительный интервал глубины L в рассмотренном примере, если доверительная вероятность g уменьшиться в 1,5 раза? Как изменится доверительная вероятность g, если в два раза увеличить число измерений?

ДоверительныЙ интервал J_g(m) = ( , )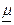

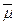Случай II (s - неизвестная величина). Будем искать симметричный ДИ в виде J_g(m) = ( 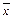-e, 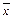+e), где 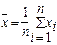- выборочное среднее параметра m. Для построения “точного” ДИ воспользуемся тем, что СВ 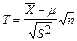~ t_n-1, где 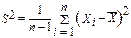- точечная оценка дисперсии D[X]. Если s_(g+1)/2 - квантиль уровня (g+1)/2 распределения Стьюдента с (n-1) степенью свободы, то справедливо следующее:

P{½T½ < s_(g+1)/2} = P{-s_(g+1)/2 < T < s_(g+1)/2} = P{T < s_(g+1)/2} - P{T < -s_(g+1)/2} = P{T < s_(g+1)/2} - P{T < s_(1-g)/2} = (g+1)/2 - (1-g)/2 = g.

Тогда P{½ 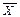-m½ < s_(g+1)/2× 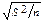} = g,

где S² - точечная оценка дисперсии D[X]. Следовательно e(g) = s_(g+1)/2× 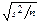, где s² - выборочное значение дисперсии D[X]. Тем самым получен ДИ для параметра m следующего вида:

J_g(m) = ( 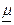, 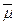) = ( 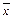-e, 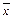+e), где 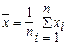, e = s_(g+1)/2× 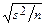и .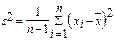

Пример. Пусть измеряемая величина X ~ N(m, s) является пределом текучести материала. По четырем испытаниям установлены: выборочное среднее 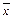= 400 МПа и выборочное значение дисперсии s² = 16 (МПа)². Требуется определить ДИ для M[X] с уровнем значимости a = 0,1.

Решение. Сначала определим квантиль уровня 0,95 распределения Стьюдента с 3 степенями свободы: s_(g+1)/2 = t_{3; 0,05} = 2,35. Следовательно J_0,9(m) = ( 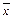- t_{3; 0,05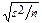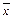} × , + t_{3; 0,05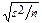} × ) = (400 - 4,7; 400 + 4,7) МПа.