Сети, потоки в сетях. Теорема Форда – Фалкерсона
Сетью называется связный граф (обычно, не орграф и не мультиграф), в котором заданы “пропускные способности” ребер, т. е. числа qij. Это числа большие или равные нулю, причем qij = 0 тогда и только тогда, когда нет ребра, соединяющего вершины i и j. Таким образом, можно считать, что пропускные способности ребер заданы для любой пары вершин. В дискретной математике пропускные способности ребер, как и все возникающие константы, считаются целыми числами (или рациональными, что одно и то же, так как рациональные числа отличаются от целых только единицами измерения). Заметим, что сети имеют огромные приложения, в частности, “сети планирования” (имеется в виду планирование производства некоторых новых, достаточно сложных изделий), где “пропускные способности” ребер – это время, за которое нужно из нескольких узлов изделия (вершин графа) получить другой (более сложный) узел. Сетевое планирование здесь не исследуется, так как гораздо больший интерес представляет сеть связи, где пропускные способности ребер – это обычно “количество одновременных разговоров”, которые могут происходить между телефонными узлами (вершинами графа).
Потоком в сети между вершиной t (источником) и s (стоком) называется набор чисел сij, (т. е. количество условного “груза”, перевозимого из вершины с номером i в вершину с номером j), удовлетворяющих четырем условиям:
1) числа сij 0, причем если сij > 0, то сji = 0 (нет встречных перевозок);
2) числа cij qij (соответствующих пропускных способностей ребер);
3) если вершина с номером i – промежуточная (не совпадает с источником и стоком), то 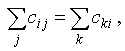 т. е. количество “груза”, вывозимого из вершины i, равно количеству “груза”, ввозимого в эту вершину;
т. е. количество “груза”, вывозимого из вершины i, равно количеству “груза”, ввозимого в эту вершину;
4) количество “груза”, вывозимого из источника t, должно быть равно количеству груза, ввозимого в сток s: 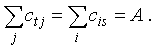
Число А называется величиной данного потока или просто потоком между t и s.
Для дальнейшего нам нужно следующее определение:
Пусть имеется некоторое сечение между вершинами t и s. Тогда величиной сечения называется сумма пропускных способностей ребер, входящих в это сечение. Сечение называется минимальным (максимальным), если его величина минимальна (максимальна).
Теорема Форда – Фалкерсона (1955). Максимальный поток между вершинами t и s равен величине минимального сечения между этими вершинами.
Доказательство этой теоремы является конструктивным (т. е. показывает, как найти нужный максимальный поток), поэтому приводится ниже.
1. Докажем сначала, что любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть дан некоторый поток и некоторое сечение. Величина данного потока складывается из величин “грузов”, перевозимых по всем возможным путям из вершины t в s. Каждый такой путь обязан иметь общее ребро с данным сечением. Так как по каждому ребру сечения суммарно нельзя перевести “груза” больше, чем его пропускная способность, поэтому сумма всех грузов меньше или равна, сумме всех пропускных способностей ребер данного сечения. Утверждение доказано.
Отсюда следует, что любой поток меньше или равен величине минимального сечения, а значит и максимальный поток меньше или равен величине минимального сечения.
2. Докажем теперь обратное неравенство. Пусть имеется некоторый поток cij (какой-то поток всегда существует, например, нулевой, когда все cij = 0). Будем помечать вершины графа, причем считаем, что все помеченные вершины образуют множество Y. Пометки вершин производятся от источника. Каждая пометка вершины (если эта вершина может быть помечена) состоит из двух чисел: первое – это “+” или “–” номер вершины (из Y), c которой связана новая помечаемая вершина, и второе – (обязательно должно быть положительным) – это фактически та добавка к потоку, которая может быть дополнительно “довезена” в эту вершину из источника по сравнению с исходным потоком.
Более точно, множество помеченных вершин Y образуется следующим образом:
источник t принадлежит Y и его пометка (0, ); второе число, условно говоря, равно бесконечности – что для дискретной математики означает, что это настолько большое число, как нам понадобится;
если вершина i принадлежит Y и cij < qij (дуга (i,j) – прямая и ненасыщенная), то вершина j также принадлежит Y и пометка вершины j равна (+i, j), где j>0 равно j= min {i, qij – cij}. Заметим, что здесь число i – это второе число уже помеченной вершины i, а знак + перед номером i означает, что дуга, связывающая вершины (i, j) является прямой (и ненасыщенной);
если вершина к принадлежит Y и сjk > 0 (обратная дуга), то вершина с номером j также должна принадлежать Y и ее пометка равна (– к, j), где знак минус означает, что вершина j связана с уже помеченной вершиной к обратной дугой, j= min{k, qjk+cjk}, причем очевидно, что j также строго больше нуля. Таким образом, построение множества Y является индуктивным, т. е. новая вершина добавляется в Y, если она связана с некоторой вершиной уже входящей в Y либо прямой ненасыщенной дугой, либо обратной дугой.
После того как построение множества Y закончено (к нему нельзя добавить новых вершин), возможны 2 случая.
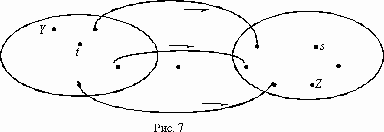
1. Сток (т. е. вершина с номером s) не входит в множество вершин Y. Тогда обозначим множество вершин, не входящих в Y через Z. Наш граф по условию является связным, поэтому из Y, в Z идут некоторые ребра. По правилам построения Y все эти ребра являются прямыми насыщенными дугами (рис. 7).
Ребра, идущие из множества Y в Z, образуют сечение между вершинами t и s. Видно также, что сумма пропускных способностей ребер этого сечения (а все эти ребра являются прямыми, насыщенными) равна потоку из t в s. Значит, данный поток является максимальным (так как он равен величине некоторого сечения), а данное сечение является минимальным.
2. Вершина s также входит в Y, и пусть второе число ее пометки s > 0. Тогда, очевидно, что между вершинами t и s существует цепь (состоящая из направленных ребер – прямых и обратных дуг), соединяющая эти вершины
Заметим, что дуга, выходящая из источника, и дуга, входящая в сток, должны быть обязательно прямыми. Прибавим s к cij для прямых дуг этой цепи (по построению видно, что полученное число будет меньше или равно qij) и вычтем это s из cij для обратных дуг (может получиться отрицательное число, но оно обязательно будет по абсолютной величине меньше qij, так как по построению s cij+qij , а это означает, что обратная дуга меняет направление, становится прямой дугой и его “нагрузка” будет равна модулю числа 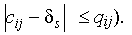 Тогда новые числа для дуг, входящих в нашу цепь, а также “старые” cij для всех дуг, не входящих в нашу цепь, образуют новый поток из вершины t в вершину s (легко проверить простым рассуждением, что для новых чисел выполняются условия (1)–(4)). Кроме того, величина нового потока по сравнению со старым увеличилась на s > 0 . Для нового потока снова проведем ту же процедуру и т. д.
Тогда новые числа для дуг, входящих в нашу цепь, а также “старые” cij для всех дуг, не входящих в нашу цепь, образуют новый поток из вершины t в вершину s (легко проверить простым рассуждением, что для новых чисел выполняются условия (1)–(4)). Кроме того, величина нового потока по сравнению со старым увеличилась на s > 0 . Для нового потока снова проведем ту же процедуру и т. д.
Так как каждый раз величина потока увеличивается, по крайней мере, на 1 (пропускные способности ребер являются целыми числами), а величина максимального потока ограничена (величиной минимального сечения), то эта процедура не может продолжаться бесконечно и, значит, на каком-то шаге получим поток, для которого вершина s не входит в Y, т. е. поток является максимальным и величина его равна величине минимального сечения. Теорема доказана.
Рассуждение теоремы Форда – Фалкерсона фактически является алгоритмом нахождения максимального потока между двумя вершинами (или доказательством того, что этот поток является максимальным).
Примечание. Если в данном графе с пропускными способностями ребер (т. е. сети) имеется несколько источников и несколько стоков, то описанный выше алгоритм можно применить следующим образом. Вводим новый источник и новый сток, причем новый источник соединяем ребрами со всеми источниками, а новый сток – со всеми стоками, при этом пропускные способности новых ребер считаем сколь угодно большими числами, так что эти дуги в любом возможном потоке были бы ненасыщенными (напомним, что ребра, идущие из источника и ребра, идущие в сток всегда являются прямыми дугами). После этого для нового графа решаем задачу о максимальном потоке (из одного нового источника в один новый сток). Решив ее, стираем все введенные ребра и вершины.
Закдание 1 требуется по данному ориентированному графу составить структурную матрицу, а по ней (методами булевой алгебры) найти все пути из вершины i в вершину j, а затем (отрицанием этих путей) найти все сечения между двумя указанными вершинами. Пусть дан ориентированный граф (рис. 12) , причем ребра a,b,h являются ориентированными (их направление указано стрелками), а остальные ребра не ориентированы. Требуется методами булевой алгебры найти пути и сечения между вершинами 2 и 4.
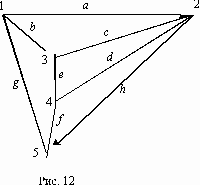
Составляем структурную матрицу S, затем вычеркиваем из нее 4-ю строчку и 2-й столбец (тем самым получаем минор М(4,2)):
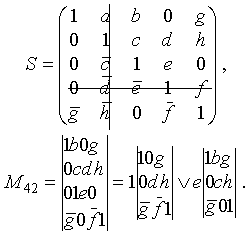 .
.
Раскрытие определителей производится по известному правилу: определитель равен сумме (в данном случае дизъюнкции) произведений элементов, умноженных на свои алгебраические дополнения (в данном случае просто миноры). При этом для определителей 3-го порядка можно пользоваться и правилом треугольника.
Тогда получаем 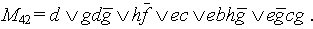
Искомые пути, расположенные в порядке прохождения ребер:
П 24 = d hf ce hgbe.
Сечения же получатся отрицанием этих путей. Применяя правила де Моргана (заменяя конъюнкцию на дизъюнкцию и наоборот), затем раскрывая скобки, получаем: (знаки отрицания опущены во всех равенствах, кроме 1-го):
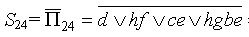 = d (h f)(c e)(h g b e)
= d (h f)(c e)(h g b e)
S24= d(h f)(e ch cg cb) = d(he ch cgh сbhfe fchfcg fcb),
или, применяя в скобках правило поглощения, получаем
S24 = d(he ch fe fcg fcb),
S24=dhedch dfе dfcg dfcb.
Задание 2 требуется найти в данной сети (т. е. в графе с заданными пропускными способностями ребер) максимальный поток из вершины с номером 1 в вершину с наибольшим номером (в заданиях либо в вершину 5, либо 6). В задании заданы 2 графа (граф, который находится слева, – это сеть с заданными пропускными способностями ребер, и граф справа с заданным потоком, который необходимо либо улучшить, либо доказать, что он не улучшаем и, значит, является максимальным). Конечно, можно дать задание просто найти максимальный поток между двумя вершинами. Однако при работе вручную нельзя дать большое число вершин (в наших заданиях это число равно 5 или 6), а в этих случаях максимальный поток можно найти без всякой теоремы Форда-Фалкерсона (просто из общих соображений). Поэтому задание в примерах 61–70 состоит в том, чтобы правильно расставить пометки для заданного потока, указанного в графе справа и после этого делать выводы о том, является ли этот поток максимальным или нет.
Задание состоит в следующем: требуется, расставляя пометки в графе
с заданным потоком с помощью алгоритма, описанного в теореме Форда – Фалкерсона, найти максимальный поток между вершиной с номером 1 и вершиной с максимальным номером. При этом если улучшенный поток окажется максимальным, то нужно указать то минимальное сечение, которому равен наш поток (если же улучшенный поток не окажется максимальным, то нужно снова его улучшать до тех пор, пока он не окажется максимальным). На рис. 13а изображен граф с данными пропускными способностями ребер, при этом вершина номер 1 является “источником”, а вершина 6 – стоком. На рис. 13б изображен тот же граф, но на ребрах его задан поток, удовлетворяющий свойствам 1–4, который надо либо увеличить, либо доказать, что он является максимальным.
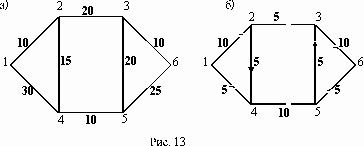
После этого подробно объясняем, как расставляются пометки в этом графе, и результат этого показываем на рис. 14. Для нового потока (рис. 14) снова расставляем пометки и убеждаемся, что этот поток является максимальным (рис. 15). Здесь же находим минимальное сечение, которому равен поток.
Начинаем расставлять пометки во втором графе (там дан поток).
1-я вершина (источник) всегда имеет пометку ( ) (это означает, что второе число как угодно большое). Далее вторую вершину пометить пока нельзя, зато можно пометить вершину 4 и ее пометка будет (+1,25). Это означает, что дуга (1,4) прямая, ненасыщенная и по ней можно “перевезти” дополнительно 25 единиц “груза”. Далее вершину 5 пометить пока нельзя, но теперь можно пометить вершину 2 и ее пометка будет (–4,20).
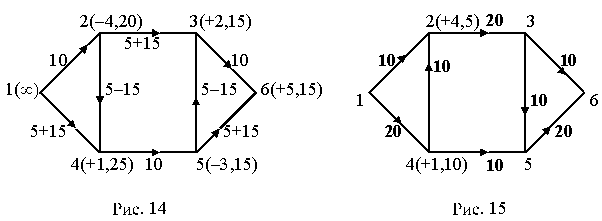
Это означает, что дуга (4,2) обратная, и, учитывая возможный “разворот” ее, по ней можно дополнительно “перевезти” 20 единиц “груза”. Так как 20 меньше 25, получаем данную пометку. Теперь можно пометить вершину 3 пометкой (+2,15) и, вершину 5, пометка которой будет (–3,15). (Заметим, что по дуге (5,3) с учетом разворота можно дополнительно “перевезти” 25 единиц груза, но так как для вершины 3 второе число было равно 15, то любое следующее число не может быть его больше). Только после этого можем пометить вершину 6 (сток), пометка которой будет (+5,15). Таким образом, наш поток можно увеличить на 15 единиц, прибавляя эти 15 единиц к прямым дугам и вычитая из обратных с учетом возможного “разворота” обратных дуг. Результат всех этих действий изображен на рис. 14.
Таким образом, получили новый поток, изображенный на рис. 15.
После этого для нового потока (рис. 15), снова расставляем пометки, которые также изображены на рис. 15. Мы видим, что для этого потока (кроме источника) можно пометить только 2 вершины: вершину 4 (ее пометка будет (+1,10)) и (после этого) вершину 2, пометка которой будет (+4,5). Больше ничего пометить нельзя, так как из множества помеченных вершин (Y) в множество непомеченных вершин (Z) идут только прямые, насыщенные дуги (дуги (2–3) и (4–5)). Эти две дуги образуют минимальное сечение, величина которого равна 30 условных единиц, и эта же величина равна величине потока. Заметим, что величина потока также равна “количеству груза”, вывозимого из источника, и равна количеству груза, ввозимого в сток. Таким образом, поток на рис. 15 является максимальным, а дуги (2–3) и (4–5) образуют минимальное сечение, которому равен наш поток.
Определение. Цепью Маркова с дискретным временемназывается цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временемназывается цепь, изменение состояний которой возможно в любые случайные моменты времени.
Определение. Однороднойназывается цепь Маркова, если условная вероятность pij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность pij называется переходной вероятностью.
Допустим, число состояний конечно и равно k.
Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:
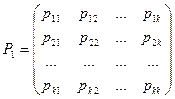
Эта матрица называется матрицей перехода системы.
Т.к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то, очевидно, что сумма элементов каждой строки матрицы равна единице.
На основе матрицы перехода системы можно построить так называемый граф состояний системы,его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.
Пример. По заданной матрице перехода построить граф состояний.
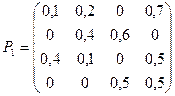
Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.

S1
0,2 0,7
S2 0,4 S4
0,6 0,5
0,1 0,5
S3
На графе не отмечаются вероятности перехода системы из одного состояния в то же самое. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.
Пусть Pij(n) – вероятность того, что в результате n испытаний система перейдет из состояния i в состояние j, r – некоторое промежуточное состояние между состояниями i и j. Вероятности перехода из одного состояния в другое pij(1) = pij.
Тогда вероятность Pij(n) может быть найдена по формуле, называемой равенством Маркова:
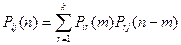
Здесь т – число шагов (испытаний), за которое система перешла из состояния i в состояние r.
В принципе, равенство Маркова есть ни что иное как несколько видоизменная формула полной вероятности.
Зная переходные вероятности (т.е. зная матрицу перехода Р1), можно найти вероятности перехода из состояния в состояние за два шага Pij(2), т.е. матрицу Р2, зная ее – найти матрицу Р3, и т.д.
Непосредственное применений полученной выше формулы не очень удобно, поэтому, можно воспользоваться приемами матричного исчисления (ведь эта формула по сути – не что иное как формула перемножения двух матриц).
Тогда в общем виде можно записать: 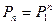
Вообще то этот факт обычно формулируется в виде теоремы, однако, ее доказательство достаточно простое, поэтому приводить его не буду.
Пример. Задана матрица переходов Р1. Найти матрицу Р3.
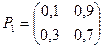
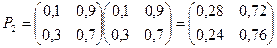
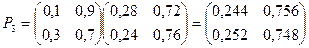
Определение. Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими. Если при некотором п все элементы матрицы Рп не равны нулю, то такая матрица переходов называется регулярной.
Другими словами, регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через п шагов из любого состояния. Такие цепи Маркова также называются регулярными.
Теорема. (теорема о предельных вероятностях) Пусть дана регулярная цепь Маркова с п состояниями и Р – ее матрица вероятностей перехода. Тогда существует предел 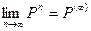 и матрица Р(¥) имеет вид:
и матрица Р(¥) имеет вид:
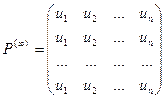
Т.е. матрица состоит из одинаковых строк.
Теперь о величинах ui. Числа u1, u2, …, un называются предельными вероятностями.Эти вероятности не зависят от исходного состояния системы и являются компонентами собственного вектора матрицы РТ (транспонированной к матрице Р).
Этот вектор полностью определяется из условий: 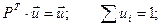
Пример. Найдем предельные вероятности для рассмотренного выше примера.
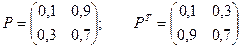
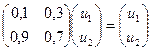
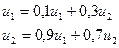
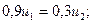
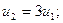
C учетом того, что u1 + u2 = 1, получаем: 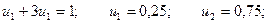
Получаем: 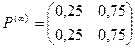
Дата добавления: 2016-06-22; просмотров: 4225;











