Методы получения Точечных оценок
Метод моментовоснован на приравнивании моментов (центральных, начальных) СВ X к их выборочным оценкам. При этом число составляемых уравнений равно числу неизвестных параметров.
Пример. Пусть Х ~ R(a, b), где a и b - неизвестные параметры. Нужно найти точечные оценки A и B параметров a и b соответственно.
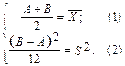
| Согласно этому методу нужно вычислить два момента (начальный 1-го порядка и центральный 2-го порядка) СВ X: mX = (a+b)/2 и DX = (b-a)2/12 и составить два уравнения (1) и (2), приравнивая моменты (A+B)/2 и (B-A)2/12 к их соответствующим выборочным значениям
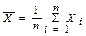 и и 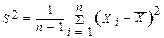 . Следовательно: . Следовательно: 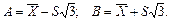
|
Метод максимального правдоподобия (Метод МП).Пусть получена конкретная выборка x1, x2, ..., xn объема n и известен закон распределения СВ X с точностью до параметров J1, J2, ..., Jk. В качестве оценок неизвестных параметров J1, J2, ..., Jk, по этому методу принимают значения Q1, Q2, ..., Qk, которые называют МП-оценками. Для их нахождения составим так называемую функцию правдоподобия:
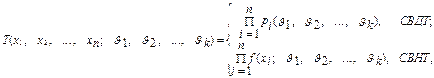
где pi(J1, J2, ..., Jk) = P{Xi = xi} - вероятность того, что СВДТ Xi примет значение xi; f(x; J1, J2, ..., Jk) - плотность распределения СВНТ X. Функция T(x1, x 2, ..., x k; J1, J2, ..., Jk) показывает, на сколько правдоподобны значения СВ X, полученные в выборке объема n при некоторых параметрах J1, J2, ..., Jk. Если J1, J2, ..., Jk - истинные значения, то, очевидно, что T(x1, x 2, ..., x k; J1, J2, ..., Jk) > T(x1, x 2, ..., x k; q1, q2, ..., qk), где q1, q2, ..., qk - значения отличные от истинных. Следовательно в качестве оценок Q1, Q2, ..., Qk неизвестных параметров выбирают такие, при которых функция правдоподобия принимает максимальное значение, т.е. T(x1, x 2, ..., x k; Q1, Q2, ..., Qk) = max. Тогда решение следующей системы из k уравнений позволяет получить оценки Q1, Q2, ..., Qk неизвестных параметров
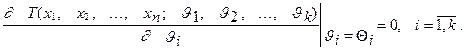
Для упрощения вычисления МП-оценок удобно рассматривать логарифм функции правдоподобия, т.е. ln T(x1, x 2, ..., x k; J1, J2, ..., Jk). Свойства МП-оценок:
n оценки являются несмещенными и состоятельными;
n при больших значениях n (n > 10 ... 20) эти оценки имеют закон распределения, близкий к нормальному.
Пример 7. С целью определения среднего трудового стажа на предприятии методом случайной повторной выборки проведено обследование трудового стажа рабочих. Из всего коллектива рабочих завода случайным образом выбрано 400 рабочих, данные о трудовом стаже которых и составили выборку. Средний по выборке стаж оказался равным 9,4 года. Считая, что трудовой стаж рабочих имеет нормальный закон распределения, определить с вероятностью 0,97 границы, в которых окажется средний трудовой стаж для всего коллектива, если известно, что s = 1,7 года.
Решение. Признак Х – трудовой стаж рабочих. Этот признак имеет нормальный закон распределения с известным параметром s = 1,7, параметр а неизвестен. Сделана выборка объемом n = 400, по данным выборки найдена точечная оценка параметра а: 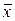 в = 9,4. С надежностью g = 0,97 найдем интервальную оценку параметра
в = 9,4. С надежностью g = 0,97 найдем интервальную оценку параметра 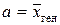 по формуле:
по формуле:
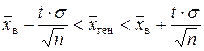 .
.
По таблице значений функции Лапласа (приложение 2) из уравнения
Ф(t) » 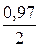 = 0,485 находим t = 2,17; тогда:
= 0,485 находим t = 2,17; тогда: 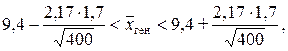
9,4 – 0,18 < 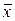 ген < 9,4 + 0,18. Итак, 9,22 <
ген < 9,4 + 0,18. Итак, 9,22 < 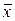 ген < 9,58, то есть средний трудовой стаж рабочих всего коллектива лежит в пределах от 9,22 года до 9,58 года (с надежностью g = 0,97).
ген < 9,58, то есть средний трудовой стаж рабочих всего коллектива лежит в пределах от 9,22 года до 9,58 года (с надежностью g = 0,97).
С изменением надежности g изменится и интервальная оценка.
Пусть g = 0,99, тогда Ф(t) = 0,495, отсюда t = 2,58. Тогда:
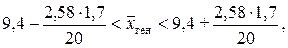 или 9,4 – 0,22 <
или 9,4 – 0,22 < 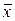 ген < 9,4 + 0,22 .
ген < 9,4 + 0,22 .
Окончательно: 9,18 < 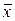 ген < 9,62.
ген < 9,62.
Пример 8. С целью определения средней продолжительности рабочего дня на предприятии методом случайной повторной выборки проведено обследование продолжительности рабочего дня сотрудников. Из всего коллектива завода случайным образом выбрано 30 сотрудников. Данные табельного учета о продолжительности рабочего дня этих сотрудников и составили выборку. Средняя по выборке продолжительность рабочего дня оказалась равной 6,85 часа, а S = 0,7 часа. Считая, что продолжительность рабочего дня имеет нормальный закон распределения, с надежностью g = 0,95 определить, в каких пределах находится действительная средняя продолжительность рабочего дня для всего коллектива данного предприятия.
Решение. Признак Х – продолжительность рабочего дня. Признак имеет нормальное распределение с неизвестными параметрами. Сделана выборка объемом n = 30, по выборочным данным найдены точечные оценки параметров распределения: 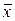 в = 6,85; S = 0,7. С надежностью g = 0,95 найдем интервальную оценку параметра
в = 6,85; S = 0,7. С надежностью g = 0,95 найдем интервальную оценку параметра 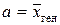 по формуле:
по формуле:
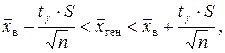
tg находим по таблице (прил. 6), tg = t(0,95; 30) = 2,045. Тогда:
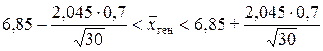 , или 6,85 – 0,26 <
, или 6,85 – 0,26 < 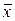 ген < 6,85 + 0,26 .
ген < 6,85 + 0,26 .
Итак, 6,59 < 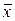 ген < 7,11 , то есть с надежностью g = 0,95 средняя продолжительность рабочего дня для всего коллектива лежит в пределах от 6,59 до 7,11 ч.
ген < 7,11 , то есть с надежностью g = 0,95 средняя продолжительность рабочего дня для всего коллектива лежит в пределах от 6,59 до 7,11 ч.
Дата добавления: 2016-06-22; просмотров: 2898;











