Электрическая проводимость растворов электролитов

В отсутствие внешнего электрического поля ионы в растворе находятся в непрерывном хаотическом тепловом движении. При возникновении разности потенциалов они приобретают направленное движение от одного полюса к другому: катионы и анионы движутся в противоположных направлениях. Таким образом, возникает электрический ток. В отличие от металлов, которые характеризуются электронным механизмом электропроводности, в растворах электролитов электричество переносится за счет движения ионов. Поэтому электролиты относят к проводникам второго рода.

Количественная характеристика способности системы проводить электрический ток – электрическая проводимость. Единицей электропроводности растворов электролитов служит удельная электрическая проводимость – величина, обратная удельному сопротивлению:

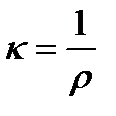, [Ом^-1м^-1 = См м^-1]

где r – удельное сопротивление

;

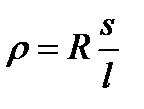R – общее сопротивление проводника, Ом;

l – длина проводника, м;

s – поперечное сечение проводника, м².

Удельная электрическая проводимость раствора электролита – это электрическая проводимость объема раствора, заключенного между двумя параллельными электродами, имеющими площадь 1 м² и расположенными на расстоянии 1 м друг от друга.

Удельная электрическая проводимость зависит от

– концентрации электролита;

– вязкости и диэлектрической проницаемости растворителя;

– температуры;

– скорости движения ионов, которая зависит от величины заряда иона и его радиуса с учетом гидратации.

С

При увеличении концентрации электролита удельная электропроводность сначала увеличивается, а затем уменьшается. Такая зависимость характерна как для сильных, так и для слабых электролитов. Это объясняется для слабых электролитов уменьшением степени диссоциации, а для сильных – электростатическим взаимодействием между ионами.

Наряду с удельной электропроводностью в электрохимии используется молярная электрическая проводимость λ – электрическая проводимость, отнесенная к числу моль растворенного вещества в 1 м³ раствора:

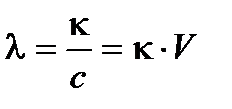, [См м² моль^-1],

где V – разведение (объем раствора, в котором содержится 1 моль электролита).

Для практических расчетов можно применять производные единицы измерения, например, если выразить концентрацию с в моль/дм³, то связь между молярной и удельной электропроводностью выражается уравнением:

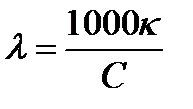; [См дм² моль^-1],

Молярная электрическая проводимость раствора электролита равна электрической проводимости объема раствора электролита, содержащего 1 моль растворенного вещества и находящегося между двумя параллельными электродами площадью 1м², расположенными на расстоянии 1 м друг от друга.

На рис. кривая I соответствует сильному электролиту, кривая II – слабому электролиту.

λ¥

I

II

λ

С

λ¥

Молярная электропроводность всегда уменьшается с увеличением концентрации электролита, что объясняется электростатическим взаимодействием между ионами. Чем больше ионов в растворе, тем меньше расстояние между ионами и сильнее взаимодействие, таким образом, ионы мешают друг другу перемещаться. С увеличением разбавления молярная электропроводность возрастает и при С ® 0 стремится к предельному значению λ_¥. (λ_¥ – предельная молярная электропроводность). Поскольку в предельно разбавленном растворе взаимодействие между ионами отсутствует, можно принять, что каждый ион движется независимо от других ионов с максимальной скоростью.

В условиях предельного разбавления выполняется закон независимого движения ионов – закон Кольрауша, согласно которому предельная молярная электропроводность раствора электролита равна сумме молярных электропроводностей катиона и аниона при бесконечном разбавлении:

,

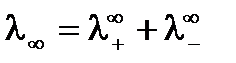где 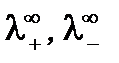- предельные электропроводности (подвижности) катиона и аниона.

Подвижность иона характеризует количество электричества, которое переносит ион и определяется абсолютной скоростью его движения (т.е. скоростью движения при напряженности электрического поля 1 В/м):

;

,

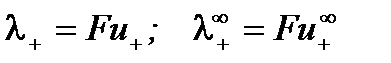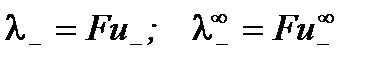где F – число Фарадея F = 96480 Кл/моль;

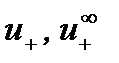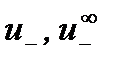, – абсолютные скорости движения катиона и аниона в растворе данной концентрации и при бесконечном разбавлении соответственно.

Абсолютная скорость движения большинства ионов равна (4 ¸ 8)10^-8 м²/(В×с). Исключение составляют только ионы Н⁺ и ОН^–, абсолютные скорости движения которых очень велики.

Абсолютные скорости движения катионов и анионов неодинаковы, то доля электричества, переносимого отдельными ионами может различаться. Для характеристики количества электричества, переносимого данным видом ионов применяют числа переноса. Число переноса – это отношение количества электричества, перенесенного данным видом ионов к общему количеству электричества, перенесенного раствором электролита. Числа переноса катионов t₊ и анионов t_– можно выразить через электропроводности:

;

.

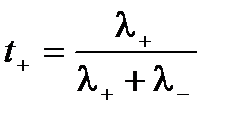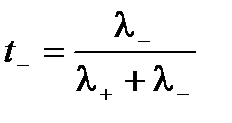Таким образом, числа переноса – это относительные подвижности ионов. Сумма чисел переноса катионов и анионов

.

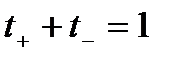Влияние межионного взаимодействия на электропроводность раствора отражает коэффициент электрической проводимости f_l:

.

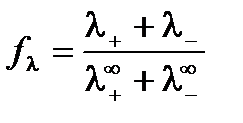Взаимосвязь l с f_l и степенью диссоциации a можно выразить уравнением:

.

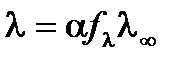Для растворов слабых электролитов межионным взаимодействием можно пренебречь, тогда f_l » 1, тогда

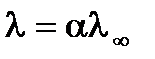
из чего следует

.

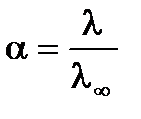Таким образом, измерив электропроводность раствора определенной концентрации, можно определить степень диссоциации электролита. Значение λ_¥ можно рассчитать по уравнению Кольрауша на основе справочных данных или определить экспериментально. Для этого измеряется электропроводность растворов слабого электролита различной концентрации. В соответствии с законом разбавления Оствальда

.

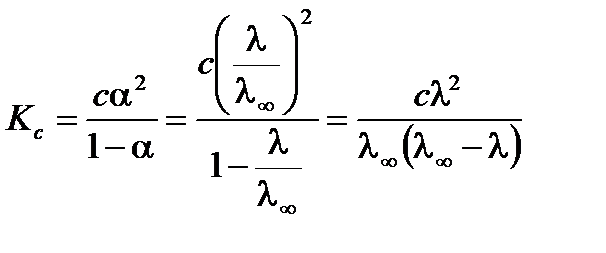Приведем уравнение к линейному виду, разделив единицу на правую и левую части:

;

.

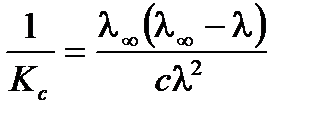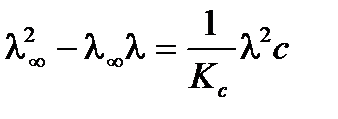Разделим на :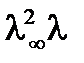

.

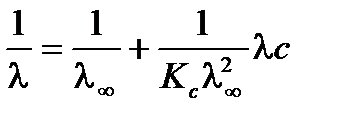а = 1/l¥

β

1/l

lс

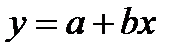Получили уравнение линейного вида , где 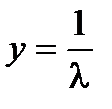, , 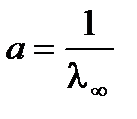, 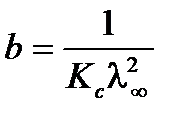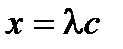. Для определения λ_¥ и К_с строится график в координатах 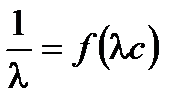, в соответствии с которым , , .

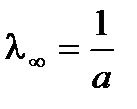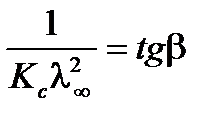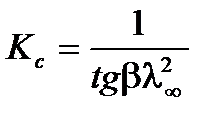Зависимость электропроводности раствора слабого электролита от концентрации можно выразить с помощью уравнения Оствальда. Для раствора слабого бинарного электролита (a << 1) в соответствии с законом разбавления Оствальда получим:

,

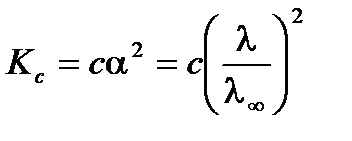тогда

.

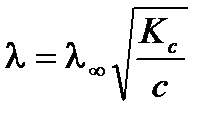Из уравнения следует, что молярная электропроводность раствора слабого электролита уменьшается с увеличением концентрации.

Для сильных электролитов α ≈ 1, тогда

;

,

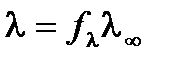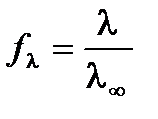следовательно, по значению электрической проводимости раствора данной концентрации можно рассчитать коэффициент электропроводности.

Зависимость молярной электропроводности раствора сильного электролита от концентрации выражается уравнением Онзагера:

,

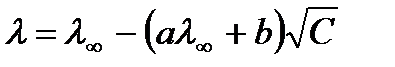где а и b – теоретические коэффициенты, зависящие от диэлектрической проницаемости растворителя, вязкости растворителя и температуры.

Как видно из уравнения Онзагера, с увеличением концентрации электролита электропроводность раствора уменьшается.

С повышением температуры электропроводность растворов электролитов увеличивается. Это объясняется понижением вязкости раствора с возрастанием температуры и увеличением скорости перемещения ионов, а для слабых электролитов также увеличением степени диссоциации.