Термодинамика гальванического элемента
Рассмотрим окислительно-восстановительную реакцию, протекающую в гальваническом элементе:
аА + bВ D сС + dD
При проведении данной реакции в условиях, максимально приближенных к обратимым можно экспериментально определить многие термодинамические характеристики данного процесса. Для того чтобы процесс протекал обратимо, он должен идти с бесконечно малой скоростью через бесконечно большое число стадий. Этого можно достигнуть, увеличив сопротивление проводника, соединяющего электроды. В этом случае реакция будет протекать медленно, а процесс будет приближаться к обратимому.
В обратимом процессе совершается максимальная электрическая работа, которая при р, Т = const равна убыли свободной энергии Гиббса:
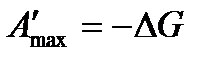 ,
,
с другой стороны в соответствии с законом Фарадея электрическая работа равна
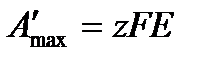 ,
,
Где z – число электронов, принимающих участие в реакции;
E – ЭДС гальванического элемента;
F – число фарадея.
Согласно уравнению изотермы химической реакции:
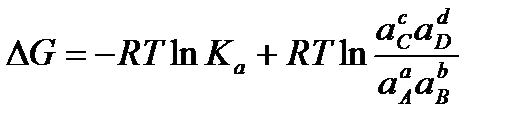 ,
,
где Ка константа равновесия реакции;
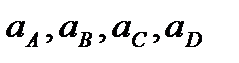 - неравновесные активности реагентов.
- неравновесные активности реагентов.
Тогда
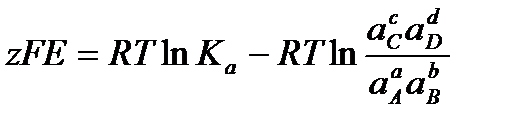
С учетом этого решим уравнение относительно Е:
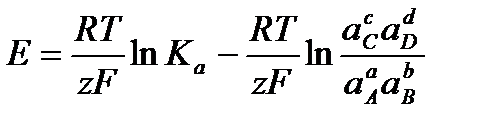 .
.
Обозначим первое слагаемое в уравнении через Е0:
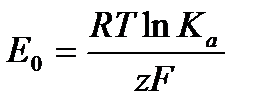 ,
,
тогда получаем
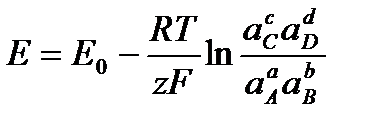 –
–
уравнение Нернста для ЭДС гальванического элемента,
где Е0 – стандартная ЭДС гальванического элемента, то есть значение ЭДС цепи при равенстве единице термодинамических активностей ионов и молекул, принимающих участие в химической реакции, лежащей в основе работы данного элемента.
На основе измерения ЭДС при различных температурах можно рассчитать изменение термодинамических функций для реакции, лежащей в основе работы элемента.
Константа равновесия реакции равна
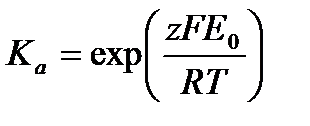 .
.
Изменение энергии Гиббса равно
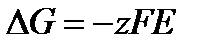 .
.
Если измерить ЭДС при нескольких температурах, то можно определить производную 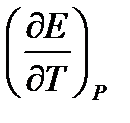 и можно рассчитать изменение энтропии:
и можно рассчитать изменение энтропии:
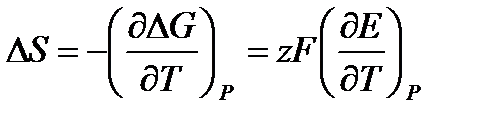
и энтальпии
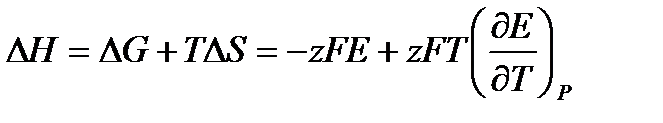
Дата добавления: 2016-06-22; просмотров: 4661;











