Понятие о резонансе в сложных цепях
Условие резонанса 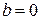 или
или 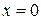 для разветвленной цепи с несколькими индуктивными и емкостными элементами, дают для частоты
для разветвленной цепи с несколькими индуктивными и емкостными элементами, дают для частоты  уравнения, которые могут иметь несколько вещественных корней, т.е. у разветвленной цепи может быть несколько резонансных частот.
уравнения, которые могут иметь несколько вещественных корней, т.е. у разветвленной цепи может быть несколько резонансных частот.
Допустим, имеется цепь, представленная на рис 3.85, потерями в которой можно пренебречь. Входное сопротивление данной цепи реактивное и равно 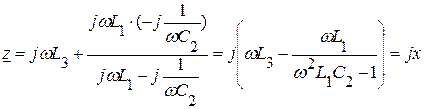 .
.

Резонанс наступает при 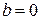 или
или 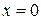 , причем если
, причем если 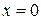 , то
, то 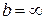 , и, наоборот, если
, и, наоборот, если 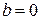 , то
, то 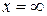 . Это справедливо всегда, если пренебречь активными сопротивлениями в ветвях. Следовательно, резонансными будут частоты, обращающие
. Это справедливо всегда, если пренебречь активными сопротивлениями в ветвях. Следовательно, резонансными будут частоты, обращающие 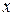 в нуль или в бесконечность. В рассматриваемом случае
в нуль или в бесконечность. В рассматриваемом случае 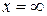 при
при 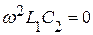 или
или 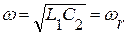 .
.
При этой частоте наступает резонанс токов в параллельных ветвях 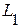 и
и 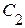 . Полагая
. Полагая 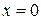 , получаем
, получаем 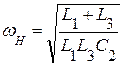 .
.
При этой частоте имеет место резонанс напряжений в последовательном контуре, состоящем из индуктивного и емкостного элементов, эквивалентной схеме двум параллельным ветвям. Таким образом, у рассматриваемой цепи две резонансные частоты: 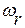 и
и 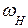 .
.
На рисунке 3.86, приведены частотные характеристики проводимостей и сопротивления рассматриваемой цепи. Кривые 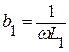 и
и 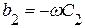 представляют характеристики проводимостей ветвей 1 и 2. Суммируя ординаты этих кривых, получаем характеристику эквивалентной проводимости
представляют характеристики проводимостей ветвей 1 и 2. Суммируя ординаты этих кривых, получаем характеристику эквивалентной проводимости 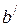 двух параллельных ветвей. Кривая
двух параллельных ветвей. Кривая 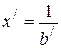 представляет эквивалентное сопротивление параллельных ветвей. Суммируя ординаты кривых
представляет эквивалентное сопротивление параллельных ветвей. Суммируя ординаты кривых 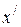 и
и 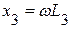 , построим характеристику входного сопротивления цепи
, построим характеристику входного сопротивления цепи 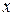 . Эта характеристика имеет две особые точки
. Эта характеристика имеет две особые точки 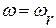 и
и 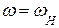 .
.
 | |||
| |||
Дата добавления: 2016-06-22; просмотров: 1995;











