Поверхностный эффект в проводе кругового сечения
Рассмотрим явление поверхностного эффекта при прохождении синусоидального тока по цилиндрическому проводу кругового сечения. Поле в проводе будет обладать цилиндрической симметрией в системе координат z, r, α. Вектор плотности тока будет иметь только z проекцию, которая будет функцией координаты r и времени t . Дифференциальное уравнение для плотности тока примет вид
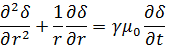
Заменяя синусоидальные функции времени комплексами действующих значений , получим
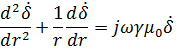
Введением новой переменной
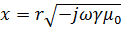
Уравнение приводится кболее простому виду
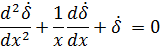
Это уравнение является частным случаем уравнения Бесселя. Его решение имеет вид
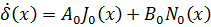
где 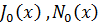 - бесселевы функции первого и второго рода нулевого порядка. Постоянные интегрирования А0, В0 находятся из граничных условий при r=0 и r=R, R – радиус провода. Из свойств функций Бесселя J0(0)=1,N0(0)=∞ , поэтому
- бесселевы функции первого и второго рода нулевого порядка. Постоянные интегрирования А0, В0 находятся из граничных условий при r=0 и r=R, R – радиус провода. Из свойств функций Бесселя J0(0)=1,N0(0)=∞ , поэтому
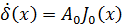
Анализ полученного выражения показывает, что величина плотности тока имеет наименьшее значение на оси провода. Ниже приведен график изменения относительного значения плотности тока в проводе в зависимости от модуля переменной х.
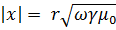
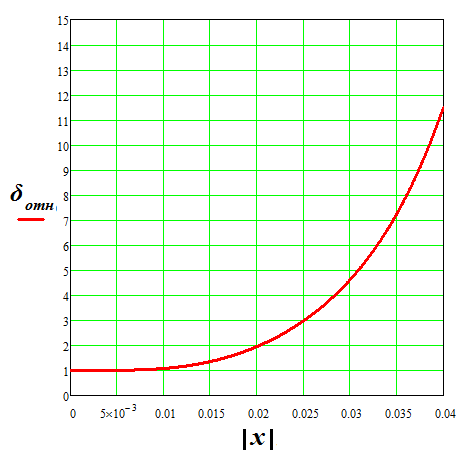
Таким образом проявление поверхностного эффекта в проводниках кругового сечения аналогичны случаю синусоидального тока в шине. С увеличением величины 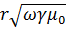 , когда ток будет распределяться только в поверхностном слое провода , его можно условно заменить эквивалентным трубчатым проводом с тем же внешним радиусом и равномерным распределением тока по сечению этой трубы. Толщину стенки трубы b, называют эквивалентной глубиной проникновения тока и рассчитывают по формуле
, когда ток будет распределяться только в поверхностном слое провода , его можно условно заменить эквивалентным трубчатым проводом с тем же внешним радиусом и равномерным распределением тока по сечению этой трубы. Толщину стенки трубы b, называют эквивалентной глубиной проникновения тока и рассчитывают по формуле
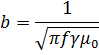
Дата добавления: 2020-03-21; просмотров: 965;











