Тема 13. Установившиеся и переходные режимы в цепях с распределенными параметрами

<33 34 353637 38 39 >

Понятие о цепи с распределенными параметрами на примере однородной длинной линии. Дифференциальные уравнения для однородной длинной линии. Первичные параметры

Набор проводников той или иной конструкции, предназначенных для направленной пространственной передачи электромагнитной энергии от одного устройства к другому назывютд линными линиями. Примером таких линий могут служить воздушные и кабельные линии связи; элементы антенных устройств, линии энергопередачи (ЛЭП) - силовые линии.

На рисунке представлено условное изображение двухпроводной длинной линии как элемента связи для передачи энергии или сигнала от источника к приемнику(нагрузке).

Длинная линия-это линейная электрическая цепь с распределенными параметрами, длина которой соизмерима с длиной волны передаваемых колебаний.

Распределенность параметров означает, что в длинной линии отсутствуют пространственные области с преимущественной локализацией либо электрического, либо магнитного полей, т.е. индуктивность, емкость и активное сопротивление распределены вдоль всей длины линии. Следовательно, схема замещения длинной линии может быть представлена в виде электрической цепи из бесконечного числа бесконечно малых по величине пассивных элементов .

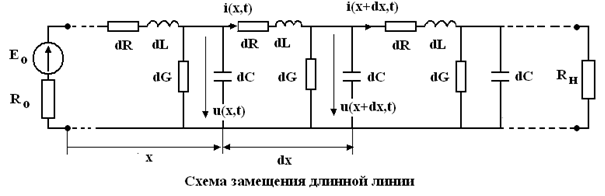
На рисунке dL, dC, dG, dR - бесконечно малые параметры длинной линии на бесконечно малом отрезке ее длины dX.

Измерять и вычислять бесконечно малые величины не представляется возможным, поэтому измеряют и вычисляют первичные параметры длинной линии на отрезке длиной либо в 1 м, либо в 1 км. По этой причине часто первичные параметры называют погонными параметрами и обозначают:

«R» - погонное сопротивление, измеряется в Ом/м или Ом/км;

«L» - погонная индуктивность, измеряется в Г/м или Г/км;

«C» - погонная емкость, измеряется в Ф/м или Ф/км;

«G» - погонная проводимость, измеряется в См/м или См/км.

Численные значения первичных параметров зависят от конструкции длинных линий. Формулы для их расчета обосновываются методами теории электромагнитного поля и приводятся в специальных справочниках по электро- и радиосвязи.

Если первичные параметры длинной линии не изменяют своих значений при их распределении вдоль направления линии, то такие линии называют однородными.

Характерным признаком длинной линии, следующим из определения, является соизмеримость ее длины с длиной волны передаваемых по ней колебаний. Это означает, что один и тот же отрезок линии для колебаний различных частот может быть длинной линией или нет. Например, отрезок воздушной линии длиной l = 0.9 м для колебаний c частотой f = 300 М Гц будет являться длинной линией, поскольку длина волны

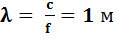
соизмерима с длиной линии l . Тот же отрезок линии для колебаний с частотой f = 300 кГц не является длинной линией, т.к. 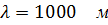, что много больше l .

Воздушная силовая линия электропередачи (ЛЭП) , работающая на промышленной частоте 50 Гц длиной 100 км , не будет считаться длинной линией, то есть цепью с распределенными параметрами, так как длина волны в ней составляет 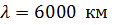, что значительно больше ее длины. Для такой линии можно использовать схему замещения с сосредоточенными параметрами R, L, C .

Конечная скорость распространения электромагнитной энергии обуславливает в длинной линии зависимость токов и напряжений не только от времени, но и от расстояния до рассматриваемой точки линии.

Определим закон изменения амплитуд и начальных фаз гармонических колебаний с изменением расстояния Х, отсчитываемого от начала линии. Используя первый и второй законы Кирхгофа для отрезка dx получим

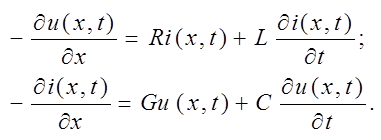
Данные уравнения есть система телеграфных(волновых) уравнений эллиптического вида математической физики.

Решение уравнений при синусоидальном процессе.

Для гармонического(синусоидального) режима работы длинной линии во времени можно перейти к комплексам амплитудных или действующих значений и тогда токи и напряжения становятся функцией только пространственной координаты x и уравнения записываются в виде

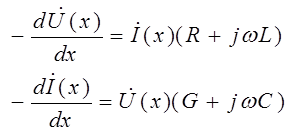
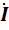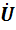Полученные дифференциальные уравнения с неизвестными и называются уравнениями передачи длинной линии. Решение этих уравнений дает следующие результаты:

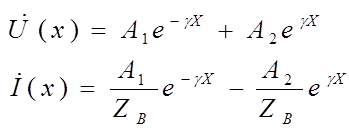
где А₁ и А₂ произвольные постоянные, зависящие от значений напряжений и токов на внешних зажимах длинной линии.

Здесь

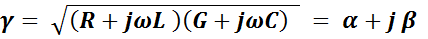
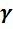- коэффициент распространения; 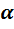- коэффициент затухания; 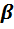- коэффициент фазы,

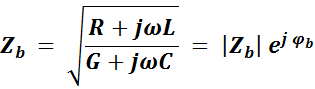
- волновое сопротивление линии.

Параметры 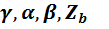- образуют группу вторичных параметров длинной линии и носят название волновых параметров.

Прямая и отраженная волны.

Определим зависимость амплитуд токов и напряжений от времени и расстояния от начала линии. Перейдем в решениях уравнений передачи длинной линии к мгновенным значениям токов и напряжений, и учтем, что

,

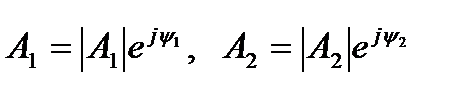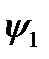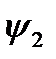где и - начальные фазы, соответствующие комплексным коэффициентам А₁ и А₂.

Тогда для мгновенных значений токов и напряжений в линии имеем:

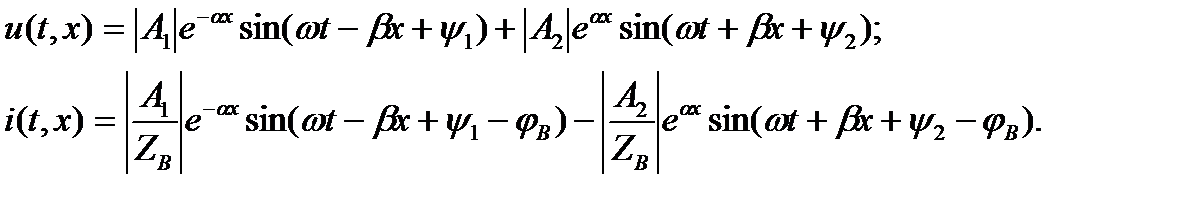
Полученные результаты подтверждают высказанное ранее предположение о зависимости токов и напряжений в линии от времени t и расстояния x . Обозначив первые слагаемые в уравнениях через 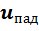и 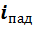, а вторые слагаемые в уравнениях через 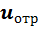и 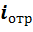, перепишем уравнения в виде:

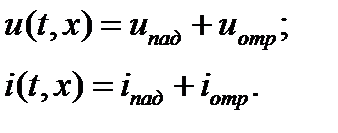
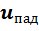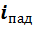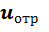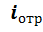Следовательно, в любом сечении линии xнапряжение и ток представляют собой сумму падающих ( и ) и отраженных ( и ) колебаний. Амплитуды колебани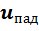й и 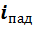убывают по мере возрастания x по экспоненциальному закону. Амплитуды колебани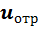й и 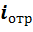возрастают по мере возрастания x по экспоненциальному закону.

Отношение амплитуд колебани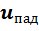й и 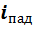в любом сечении равно 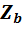, а разность фаз этих колебаний .

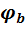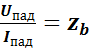
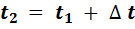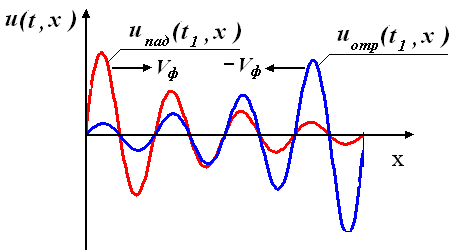
Для двух фиксированных и близких моментов времени t₁ и t₂ , таких, что распределения напряжения 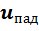вдоль линии отличаются смещением в пространстве вдоль оси x . Этот эффект воспринимается как перемещение распределения этого напряжения по направлению от начала линии к ее концу. В связи с этим это слагаемое напряжения в решении называют прямая или падающая волна. График распределения напряжения 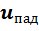вдоль оси x при фиксированном моменте времени представляет из себя синусоиду с амплитудой, затухающей по экспоненциальному закону.

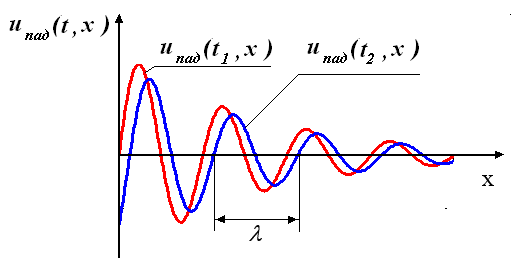
Длина волны распространяющегося по линии колебания - это период этого колебания, то есть период пространственной синусоидальной функции. Он находится как расстояние по оси x между точками графика распределения, фаза колебания которых отличается на .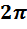

По аналогии с синусоидальными функциями времени, где период

,

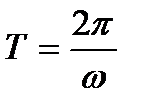можно записать для периода пространственной синусоидальной функции, обозначаемой как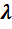

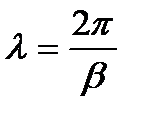
Падающая волна движется вдоль линии с определенной скоростью, которая представляет собой скорость распространения электромагнитной энергии в линии. Эта скорость определяется соотношением

.

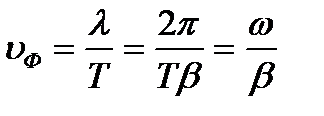Для двухпроводной воздушной линии, у которой вклады от первичных параметров R и G , отвечающих за тепловые потери малы по сравнению с вкладами от параметров L , C можно считать, что

, .

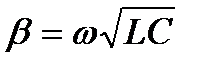С учетом выражений для индуктивности L и емкости C двухпроводной воздушной линии, взятых из справочника, получим

,

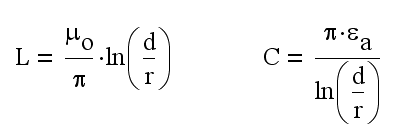
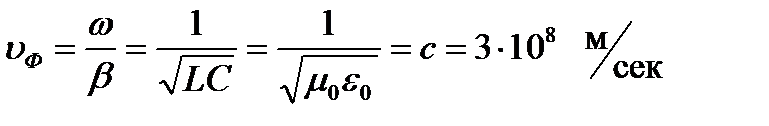где: С - скорость света в воздушном пространстве .

Для кабельных линий, где относительная диэлектрическая проницаемость

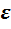диэлектрика больше единицы, скорость распространения волн вдоль длинной линии зависит от типа диэлектрика и , следовательно , меньше скорости света.

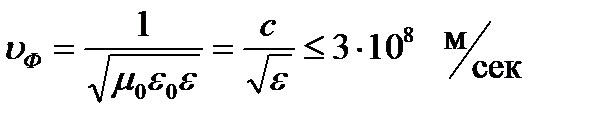
Для вторых слагаемых напряжения и тока в решениях уравнений передачи длинной линии, справедливо все сказанное выше, если учесть, что отраженная волна распространяется от конца линии к ее началу.

Ниже приведены графики распределения падающей и отраженной волн вдоль линии для некоторого фиксированного момента времени t₁ .

После введения понятий падающей и отраженной волн решение уравнений передачи можно записать так:

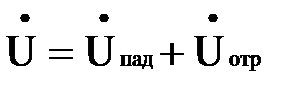
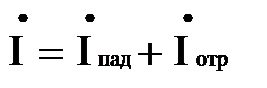
Характеристические параметры однородной линии. Волновое сопротивление, коэффициент распространения. Согласованная нагрузка.

Установим соотношения между комплексными амплитудами падающей и отраженной волн в линии длиной l нагруженной на комплексное сопротивление Z_н .

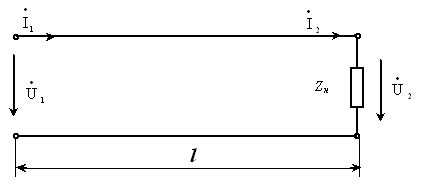
При известных значениях 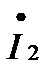и 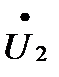положив в уравнениях х = l , получаем:

,

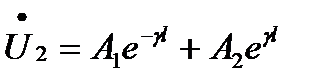
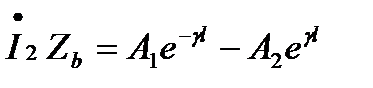откуда определим постоянные А₁и А₂

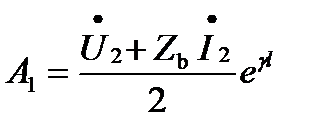
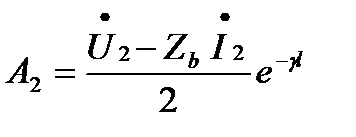
После подстановки постоянных А₁и А₂в общее решение уравнений получаем:

,

,

,

.

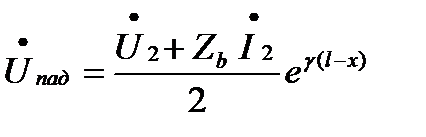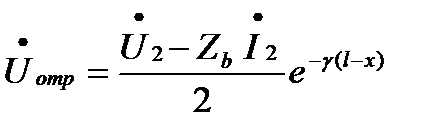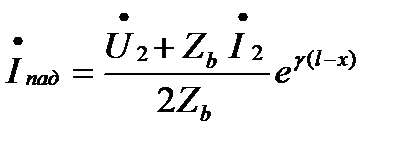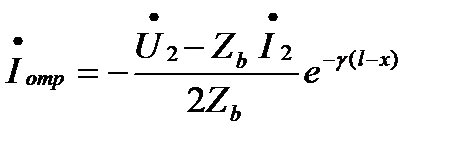Отношение:

.

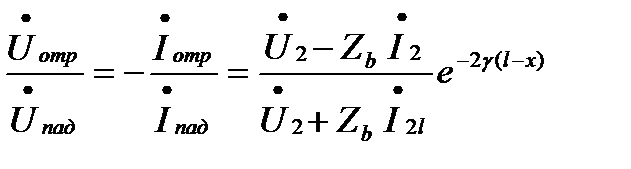При х=l это отношение получило название коэффициента отражения, обозначаемого как К_отр.

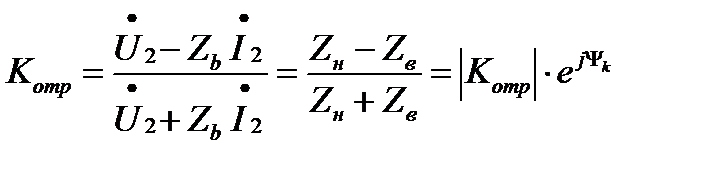
где 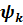- сдвиг фаз между падающей и отраженной волной в конце линии.

С учетом К_отр_. решение для комплексных амплитуд напряжений и токов приобретает вид:

,

.

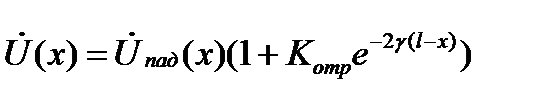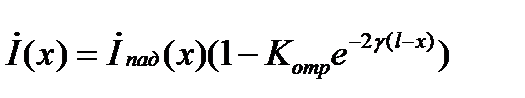Для практических расчетов важными являются случаи, когда

Z_н=Z_в - режим согласованной нагрузки,

Z_н=0 - режим короткого замыкания,

Z_н= 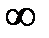- режим холостого хода .

1. При Z_н=Z_в , К_отр.=0

Тогда

, , , .

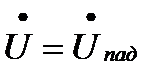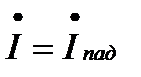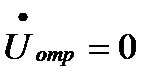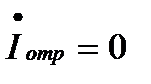Следовательно, в этом случае отсутствует отраженная волна тока и напряжения и вся энергия, передаваемая по линии, поглощается нагрузкой. Такая нагрузка называется согласованной.

2. При Z_н=0, К_отр.=-1 (режим КЗ в конце линии)

В этом случае

,

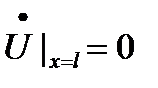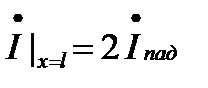
Это означает, что в режиме короткого замыкания гармонические напряжения падающей и отраженной волн в конце линии находятся в противофазе, а токи – совпадают по фазе.

3.При Z_н= 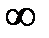, К_отр.=1 (режим ХХ в конце линии)

В этом случае

,

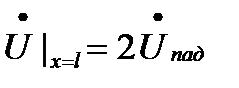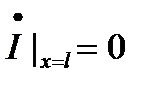
Следовательно, при отключенной нагрузке гармонические напряжения падающей и отраженной волн в конце линии находятся в фазе, а токи – в противофазе.

Произведение коэффициента распространения 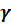на длину линии l называется постоянной передачи линии. Она представляет собой безразмерную комплексную величину

,

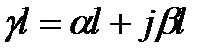где

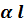- собственное, волновое или характеристическое затухание,

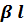- собственная, волновая или характеристическая фаза линии.

Собственное затухание линии и собственная фаза линии характеризуют способность линии передавать колебание в режиме согласованной нагрузки

Амплитудно-частотная и фазочастотная характеристики согласованно нагруженной линии определяются следующими соотношениями:

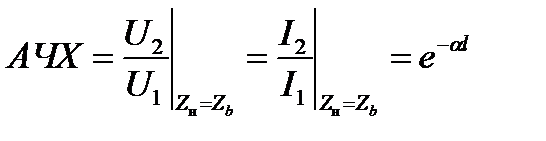
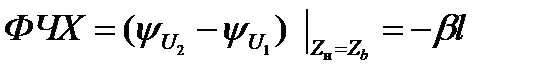
Поскольку 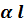и 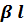зависят от частоты, то при прохождении сигнала через длинную линии нарушаются соотношения между амплитудами и фазами отдельных частотных составляющих сигнала, что вызывает амплитудные и фазовые искажения.

Входное сопротивление

Важным параметром длинной линии является его входное сопротивление Z_вх

.

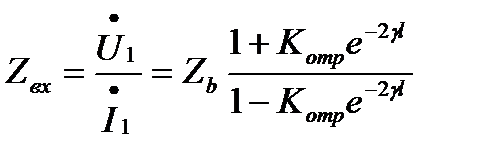При согласованной нагрузке когда К_отр = 0

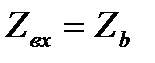
Согласованная нагрузка для ДЛ является оптимальной, т.к. в этом случае отсутствует отраженная волна и вся энергия передаваемая по линии, поглощается нагрузкой.

Линия без искажений

Линия без искажений представляет собой линию, вдоль которой волны разных частот распространяются с одинаковой фазовой скоростью и затухают в равной степени. Для того чтобы линия была неискажающей , коэффициент затухания и фазовая скорость не должны зависеть от частоты. Это возможно если между первичными параметрами линии выполняется соотношение

.

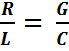Используя выражение для коэффициента распространения 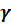,получим

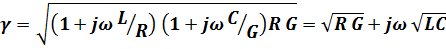
Тогда

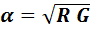
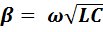
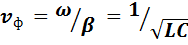
В линии без искажений волновое сопротивление

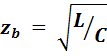
является действительным числом и также не зависит от частоты.

Линия без потерь

Линия без потерь – это линия, у которой рассеяние энергии отсутствует, что имеет место при значениях первичных параметров R=0 и G=0, где R – сопротивление проводов, G – проводимость изоляции на единицу длины линии. Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах и поэтому резистивными сопротивлением проводов и проводимостью изоляции можно пренебречь по сравнению с индуктивным сопротивлением и емкостной проводимостью линии.

Коэффициент распространения линии без потерь

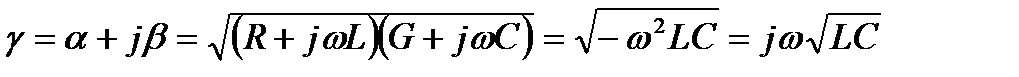
Следовательно, коэффициент затухания

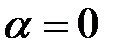
а коэффициент фазы линейно зависит от частоты.

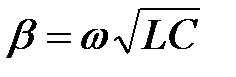
Волновое сопротивление линии без потерь

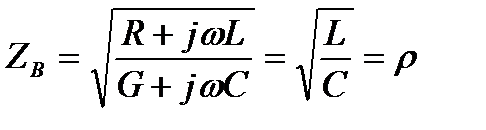
является чисто активным (резистивным) сопротивлением.

Коэффициент фазы 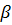связан с длиной волны электромагнитного колебания 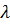известным соотношением

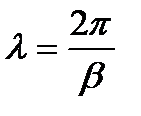
Уравнения передачи линии без потерь можно представить в виде

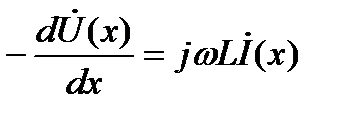
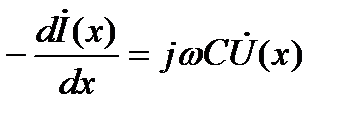
При анализе процессов, происходящих в линии без потерь, общепринято расположение той или иной точки на линии характеризовать ее удалением не от начала линии x , как это делали прежде, а от конца линии y .

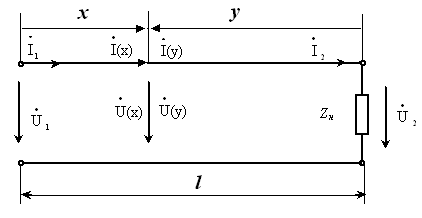
В этом случае решение уравнений передачи линии без потерь для комплексов амплитудных значений напряжения и тока в произвольной точке линии y , отсчитанной от ее конца, записываются в виде:

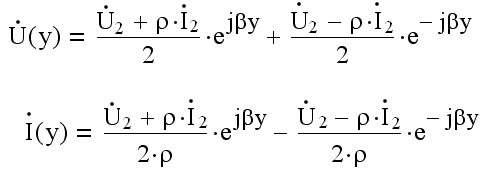
Можно выделить три типа режимов работы длинной линии без потерь. К ним относятся : режим бегущей волны, режим стоячей волны, режим смешанной волны.

<33 34 353637 38 39 >

Дата добавления: 2020-03-21; просмотров: 755;