Тема 11. Нелинейные электрические цепи переменного тока


Электрические цепи с ферромагнитными сердечниками при синусоидальных напряжениях.

Нелинейные сопротивления для переменного тока подразделяются на активные, индуктивные и емкостные. Под нелинейной индуктивностью понимают индуктивную катушку с обмоткой намотанной на сердечник из ферромагнитного материала, для которого зависимость магнитного потока в сердечнике от протекающего по обмотке тока нелинейна. Индуктивную катушку со стальным сердечником называют иногда дросселем. В электрических схемах нелинейную индуктивность изображают в виде

Все методы анализа нелинейных цепей можно подразделить на две большие группы: аналитическую и графическую. Недостатком аналитических методов является то, что приходится выражать аналитически характеристики нелинейных сопротивлений, а это всегда связано с некоторой погрешностью. Наиболее широко распространен графический метод при использовании характеристик нелинейных сопротивлений для мгновенных значений. Этот метод применим, как правило, к цепям, в которых известен закон изменения во времени какой- либо одной определяющей работу нелинейного сопротивления величины, например тока, напряжения.

Рассмотрим дроссель с ферромагнитным сердечником при подключении его обмотки к источнику синусоидального напряжения (рис.1).

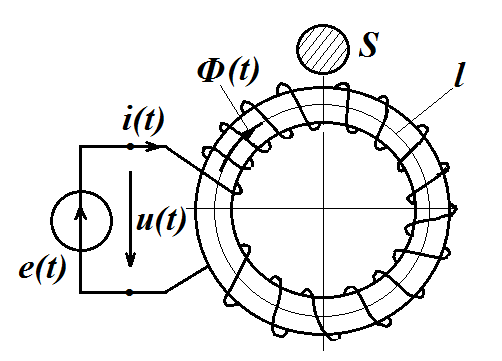
рис.1

Заданы:

l – длина средней линии;

S - сечение сердечника;

w– число витков катушки;

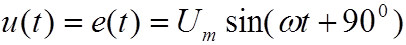
Основная кривая намагничивания материала ферромагнетика- B(H)

Рассчитать и построить график тока в обмотке i(t).

Для контура цепи обмотки по второму закону Кирхгофа можно записать

 

,

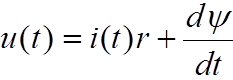где потокосцепление катушки .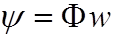

Если пренебречь сопротивлением проводов обмотки r , то

,

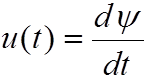тогда

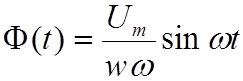
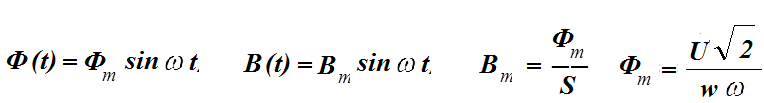
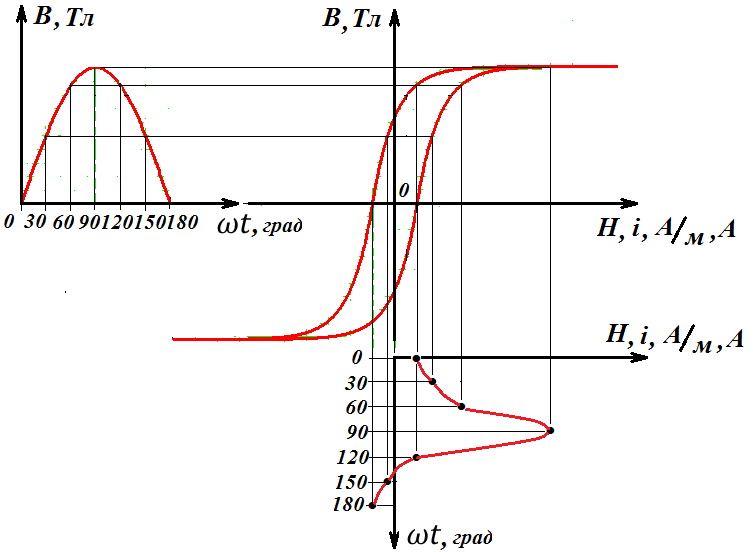
Зная значения магнитной индукции влюбой момент времени на отрезке периода ее функции и, используя кривую намагничивания ферромагнитного сердечника, с помощью графических построений получим график распределения напряженности магнитного поля во времени (рис.2).

 

 

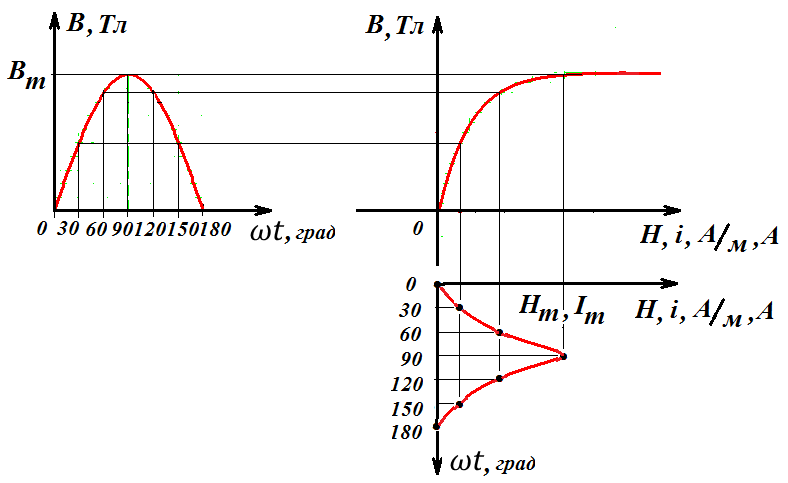
Из закона полного тока для контура, совпадающего со средней линией сердечника, получим график тока в катушке от времени (рис.2).

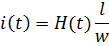
Отметим, что на рис.2 временные функции B(t), H(t), i(t) изображены только на половине периода – Т/2, что связано с симметрией этих функций.

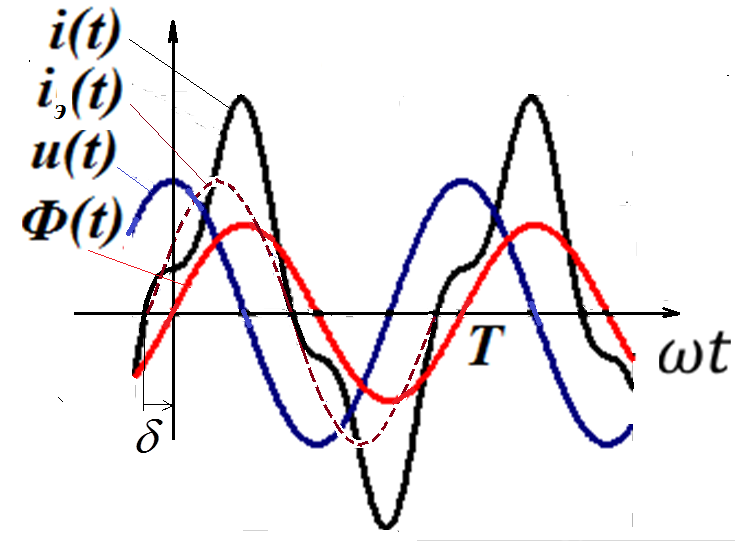
Таким образом временные графики тока , напряжения и магнитного потока в катушке и сердечнике без учета гистерезиса и вихревых токов сердечника имеют вид

 

 

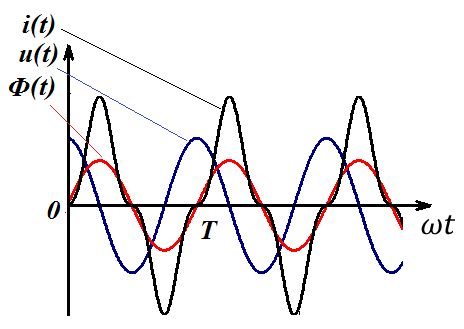
Потери на гистерезис и вихревые токи

Потери в стали (ферромагнитном сердечнике) складываются из потерь на гистерезис ( перемагничиавние) и потерь на вихревые токи, наводимые переменным магнитным полем, в стали, которая является проводником.

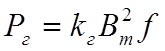
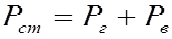
- удельные потери на гистерезис, Вт/кг

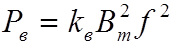- удельные потери на вихревые токи, Вт/кг

Потери в стали в ферромагнетиках проявляются в характеристиках кривых намагничивания. В этом случае кривая намагничивания имеет форму петли в технической литературе называемой петлей гистерехиса. Формакривой тока в катушке с сердечником при синусоидальном напряжении в этом случае будет иметь вид в соответствии с графическиим расчетом тока в катушке с учетом гистерезиса и вихревых токов сердечника.

 

 

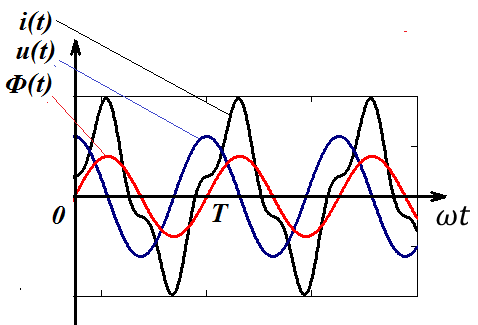
Совмещенные временные графики тока , напряжения и магнитного потока в катушке и сердечнике с учетом гистерезиса и вихревых токов .

 

Если катушка с ферромагнитным сердечником питается от синусоидального источника тока

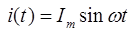
Тогда по закону полного тока для контура l в сердечнике:

 

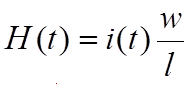
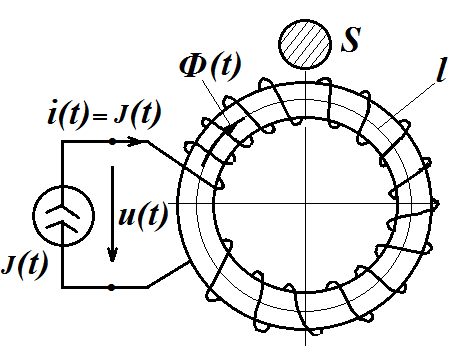
И графический расчет напряжения на зажимах катушки без учетом гистерезиса и вихревых токов сердечника дает следующие результаты

 

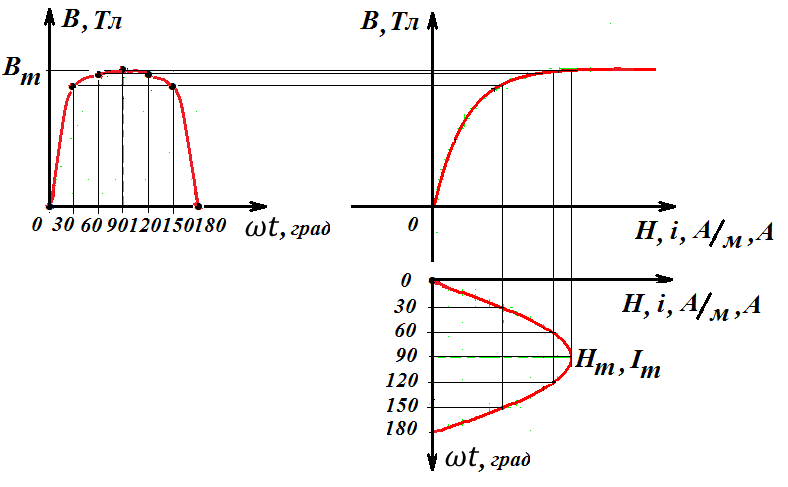
Напряжение на зажимах катушки определится графическим дифференцированием полученной зависимости B(t)

 

 

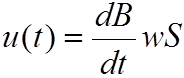
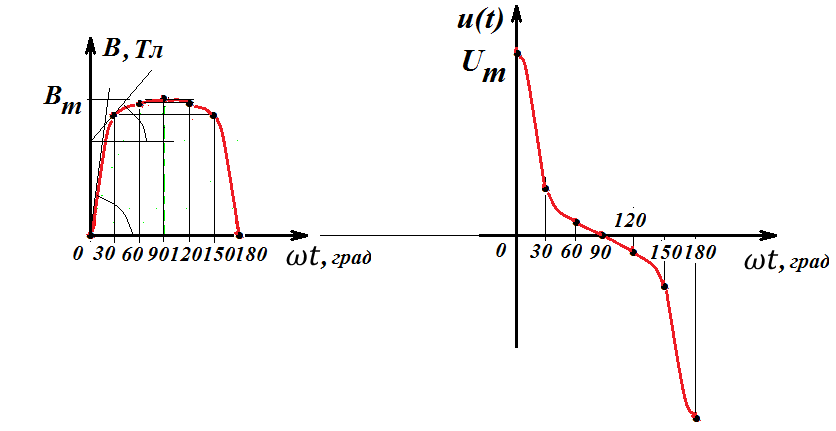
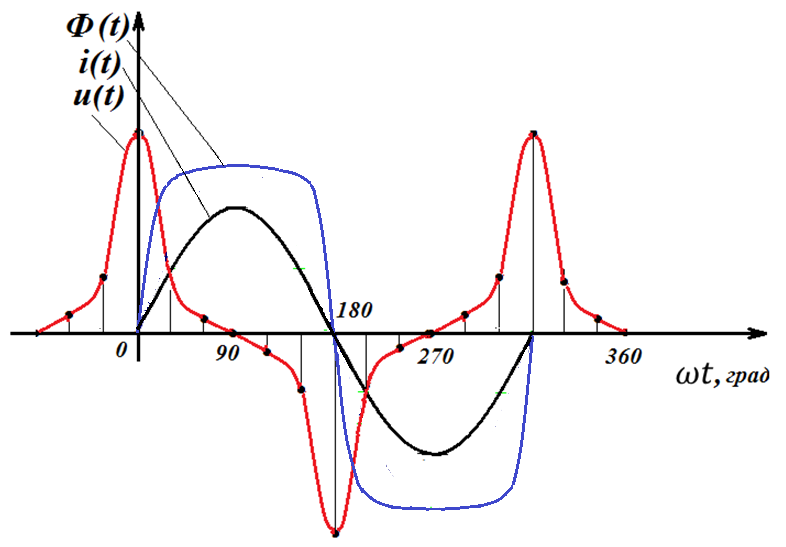
Совмещенные графики напряжения, тока и магнитного потока при питании катушки от источника синусоидального тока имеют вид

 

Расчет методом эквивалентных синусоид.

Для инженерных расчетов катушек с ферромагнитными сердечниками вместо графического метода, рассмотренного выше, используется упрощенный метод, называемый метод эквивалентных синусоид. Суть метода заключается в замене несинусоидальных функций эквивалентными синусоидальными. Условием такой замены является сохранение действующего значения несинусоидальной функции.

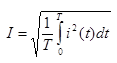
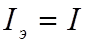
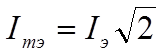
После замены несинусоидальных функций эквивалентными синусоидальными все временные функции в катушке со сталью (ток , напряжение , магнитный поток в сердечнике, магнитная индукция, магнитная напряженность) будут синусоидальными функциями времени и поэтому можно их заменить комплексами действующих значений

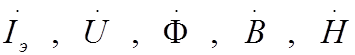
Электрическая схема замещения катушки с сердечником при синусоидальном напряжении. Векторная диаграмма.

При питании катушки от источника синусоидального напряжения векторная диаграмма комплексов имеет вид

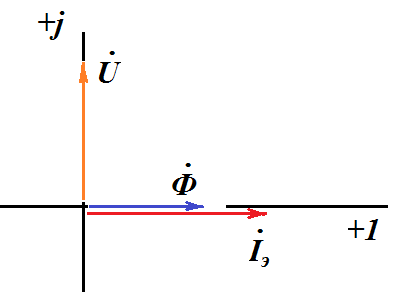
Представленная векторная диаграмма соответствует комплексной схеме замещения цепи катушки со сталью без учета потерь в стали

Эквивалентная синусоида тока в цепи катушки со сталью с учетом потерь в стали

где 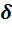- угол потерь в стали.

Векторная диаграмма и схема замещения цепи катушки со сталью с учетом потерь в стали по методу эквивалентных синусоид будет иметь следующий вид

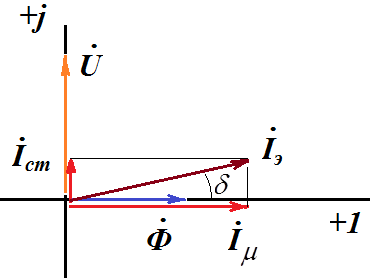
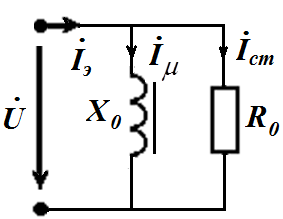
Ток в катушке можно разложить на две составляющие:

ток 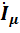-ток намагничивания;

ток 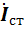- ток, учитывающий потери в стали.

 

Эти токи связаны с параметрами схемы замещения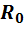

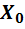
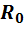- сопротивление, учитывающее потери в стали,

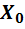- сопротивление, учитывающее энергию магнитного поля в сердечнике катушки.

Потери активной и реактивной мощностей в стали связаны с параметрами параллельной схемы замещения катушки со сталью .


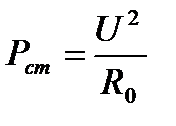
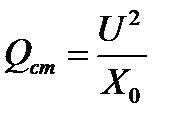
Удельные потери активной и реактивной мощностей в стали приводятся в справочной литературе в виде графиков ( в зависимости от магнитной индукции для промышленной частоты 50 Гц и для различных сортов электротехнической стали).

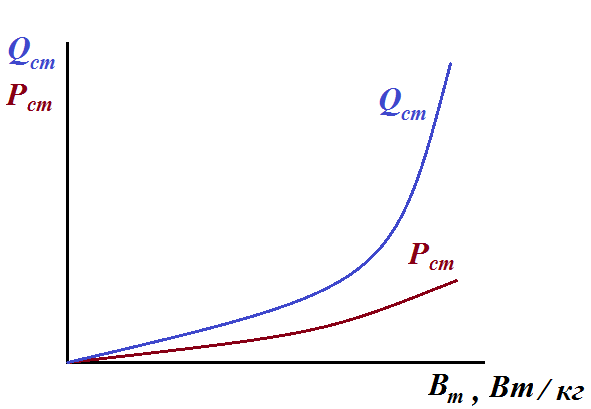В этом случае параметры схемы

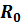
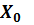
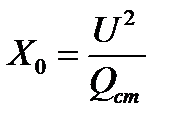
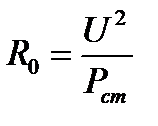находятся по формулам

 

 

Более точно параметры найдутся из графического расчета, представленного выше при использовании метода эквивалентных синусоид

 

 

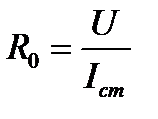
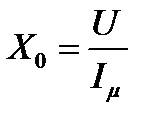
Если учесть и сопротивление проводов (витков) катушки, то схема замещения и векторная диаграмма примут вид

 

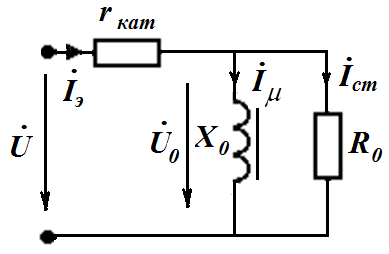
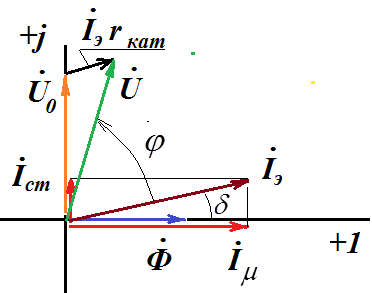
где 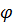- угол сдвига фаз тока и напряжения на входе катушки

Схема замещения магнитной цепи катушки со сталью в комплексной форме примет вид

 

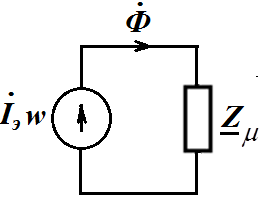
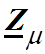- комплексное сопротивление магнитной цепи

катушки


 

 


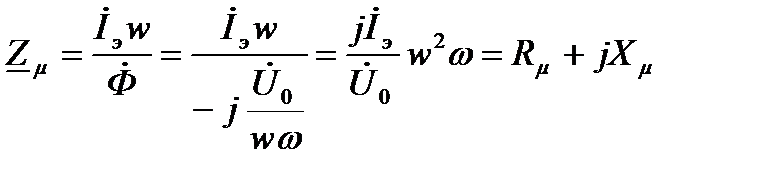
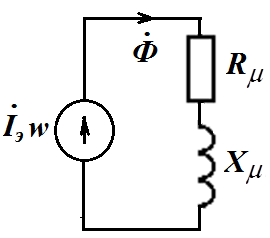
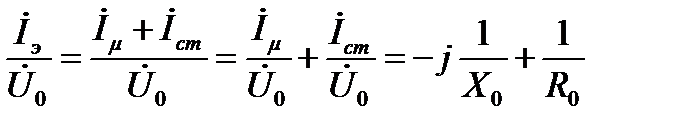
Следовательно , параметры электрической схемы замещения катушки связаны с параметрами ее магнитной схемы замещения формулами

 


 

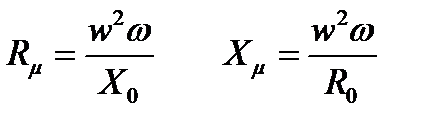
Двухобмоточный трансформатор. Опытное определение параметров схемы замещения трансформатора.

 

 

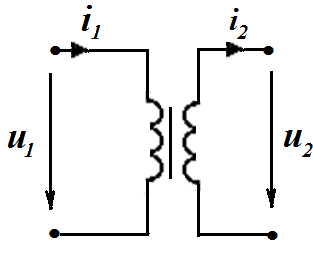Принцип действия двух обмоточного трансформатора с ферроиагнитным сердечником ничем не отличается от воздушного трансформатора. Водушный трансформатор обеспечивает линейную связь между токами и напряжениями в обмотках такого трансформатора и синусоидальность этих величин как функций времени. Ферромагнитный сердечник, как было отмечено выше, позводляет усиливать магнитное поле и создавать его концентрацию в требуемых областях пространства. При этом проявляется нелинейность ферромагнитного сердечника и, как следствие, токи и напряжения могут становиться несинусоидальными функциями времени, что было видно на примере работы дросселя.

По аналогии с рассмотрением работы дросселя с ферромагнитным сердечником составим уравнения Кирхгофа для первичной и вторичной обмоток трансформатора для мгновенных значений при питании первичной обмотки от источника синусоидального напряжения.

 


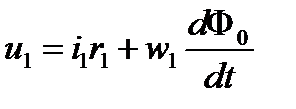
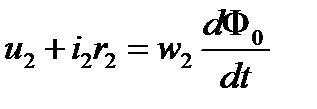
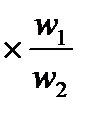
Если умножить второе уравнение на отношение числа витков первичной и вторичной обмоток, то получится приведенное уравнение к виткам первичной обмотки.

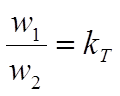
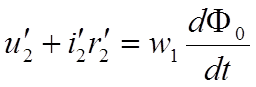
- коэффициент трансформации.

 


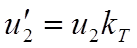
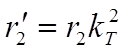
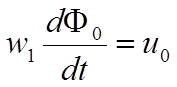
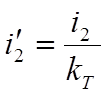
- приведенные значения тока, напряжения, сопротивления вторичной обмотки к числу витков первичной обмотки трансформатора .

Напряжение 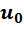связано с магнитным потоком в сердечнике трансформатора 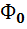также, как и в катушке со сталью. Эти величины определяют цепь намагничивания трансформатора.

Заменим несинусоидальные токи в обмотках трансформатора эквивалентными синусоидами, как это проделано в катушке со сталью, и запишем приведенные уравнения Кирхгофа в комплексной форме.

 

 

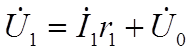
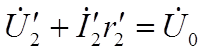
Полученным уравнениям соответствует комплексная схема замещения приведенного трансформатора и векторная диаграмма.

 

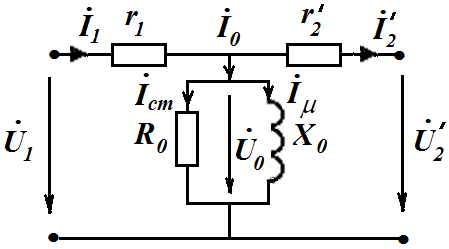
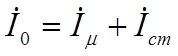
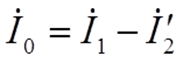
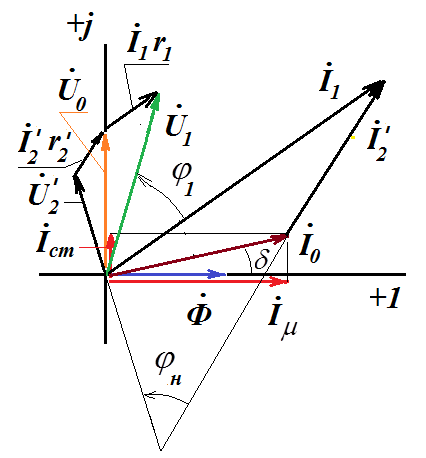
Параметры схемы замещения трансформатора.можно определить экспериментально, учитывая, что сопротивления обмоток значительно меньше сопротивления намагничивающей цепи. Из схемы замещения очевидно, что для этого необходимо провести опыты короткого замыкания и холостого хода.

В режиме холостого хода схема замещения трансформатора имеет вид

 

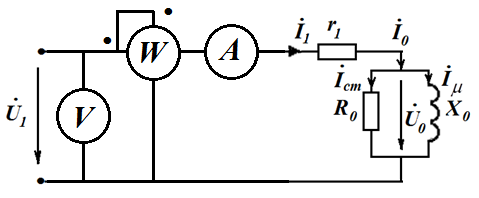
По показаниям приборов при условии пренебрежения сопротивлением r1 находятся значенния R0 , X0 .

В режиме короткого замыкания схема замещения трансформатора прнимает вид

 

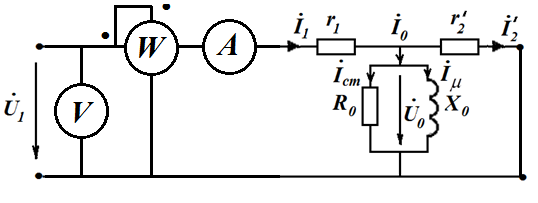
В этом опыте можно пренебречь ветвью с током I0 , так как ее проводимость на порядок меньше проводимости параллельной ветви с приведенным сопротивлением вторичной обмотки. В этом случае по показаниям приборов находится суммарное сопротивление и при условии равенства сопротивлений первичной и приведенной вторичной обмоток находятся сопртивления обмоток .

 

Явление феррорезонанса.

 

В электрических цепях, содержащих катушки с ферромагнитными сердечниками и конденсаторы, наблюдаются особые явления, связанные с нелиней ными свойствами этих цепей. Рассмотрим эти явления на примере простейшей цепи с последовательным соединением катушки с ферромагнитным сердечником и конденсатора,

 

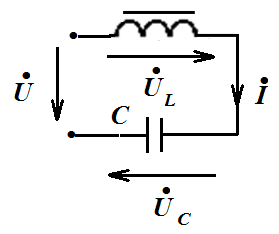
Предположим , что в цепи отсутствуют потери и заменим несинусоидальные ток и напряжения, появляющиеся в вследствии нелинейности катушки с ферромагнитным сердечником эквивалентными синусоидами в соответствием с методом эквивалентных синусоид, рассмотренным ранее. Цепь подключена к источнику синусоидального напряжения. Воспользуемся для расчета комплнксным методом, заменив синусоидальные величины на комплексы действующих значений. При любом значении тока напряжения на индуктивности и емкости будут находиться в противофазе и вследствии этого величина входного напряжения будет равна

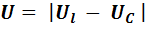
Изобразим вольт-амперные характерстики нелинейной индуктивности и линейной емкости

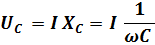
и построим результирующую зависимость входного напряжения от тока цепи U = f( I ).

 

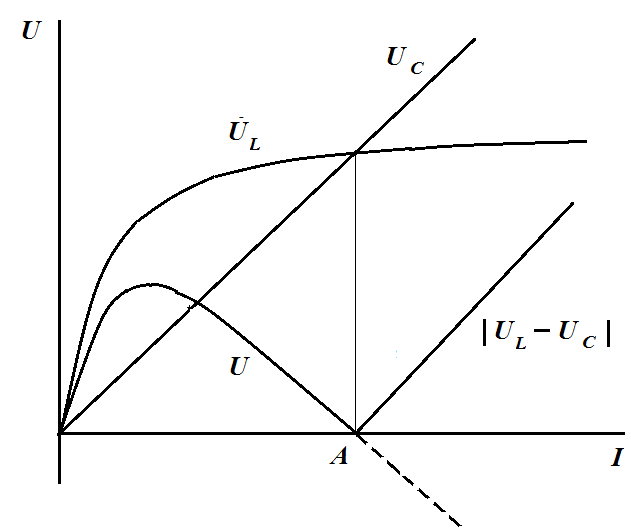
Особая точка А характеристики U = f( I ) , лежащая на оси абсцисс, является точкой резонанса, так как в этой точке напряжения UL и UC взаимно компенсируются.

В отличие от цепей с линейными элементами, резонанса в рассматриваемой цепи можно достичь изменением величины приложенного напряжения. Явление резонанса в данной цепи называют феррорезонансом в последовательной цепи.

Если учесть влияние активного сопротивления цепи r, то график зависимости

U = f( I ) примет вид

 

 

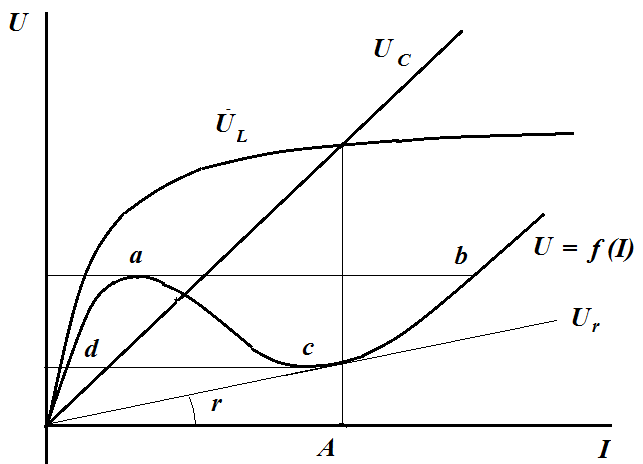
При постепенном повышении входного напряжения, мы дойдем до точки а , а далее произойдет срыв из точки а в точку b , сопровождающийся резким увеличением тока. При дальнейшем повышении напряжения увеличение тока происходит плавно. При понижении напряжения ток плавно уменьшается ло лостижения точки с характеристики, в которой происходит срыв в точку d, сопровождающийся резким уменьшением тока. Эти срывы сопровождаются изменением знака угла сдвига фаз в цепи.

Отметим, что для учета напряжения на сопротивлении r, следует вычислять входное напряжение U при выбранном на оси абсцисс токе I по формуле

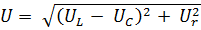
На рисунке выше приведена найденная таким методом ВАХ цепи.

 

Феррорезонансные стабилизаторы напряжения.

 

Особенности цепей, содержащих катушки с ферромагнитным сердечником и конденсатор, используют для устройства ферромагнитных стабилизаторов напряжения, служащих для поддержания постоянства напряжения на зажимах приемника при изменении напряжения питающей цепи. Рассмотрим простейший стабилизатор состоящий из последовательно соединенных между собой катушки с ферромагнитным сердечником и конденсатора. Напряжение U1 сети подводят к зажимам этой цепи, а зажимы катушки являются выходными зажимами стабилизатора с напряжением U2 .

 

 

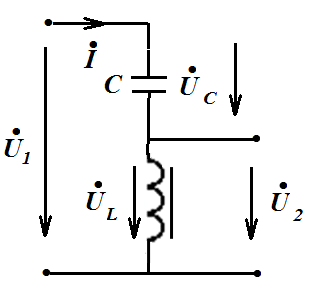
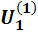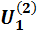При изменении напряжения сети от до выходное напряжение изменяется от 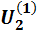до .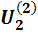

 

 

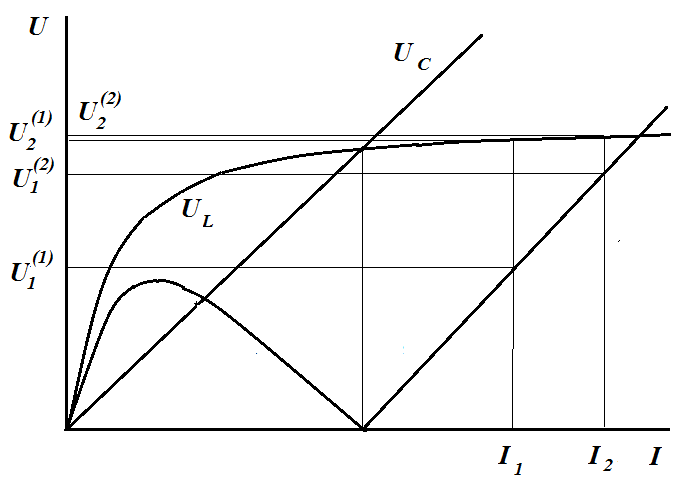
Ток в цепи при этом меняется от I1 ло I2 .

Из графиков видно, что значительное изменение напряжения сети влечет за собой сравнительно малое изменение выходного напряжения.

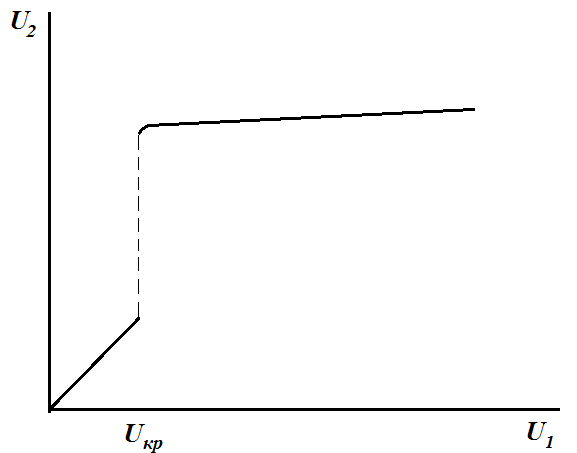
Определив для ряда значений U1 соответствующие значения U2 можно построить зависимость U2 = F( U1) , из которого видно, что рассматриваемая схема может стабилизировать напрядение только при напряжениях сети , превышающих критическое напряжение Uкр .

 

 

Включение катушки с сердечником (ненагруженного трансформатора) на синусоидальное напряжение. «Бросок намагничивающего тока». Роль остаточной индукции.

 


Дата добавления: 2020-03-21; просмотров: 1147;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.028 сек.