Включение линии на реактивное сопротивление.
Пусть линия нагружена на индуктивность Lн . При заданной частоте 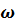 сопротивление нагрузки
сопротивление нагрузки 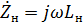 Из нижеследующего рисунка видно, что отрезок закороченной линии длиной меньше
Из нижеследующего рисунка видно, что отрезок закороченной линии длиной меньше 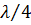 имеет входное сопротивление индуктивного характера. Поэтому всегда можно подобрать такую длину отрезка l, при которой его входное сопротивление равнялось бы заданному сопротивлению
имеет входное сопротивление индуктивного характера. Поэтому всегда можно подобрать такую длину отрезка l, при которой его входное сопротивление равнялось бы заданному сопротивлению 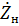 . Заменим индуктивность Lн отрезком КЗ линии . Эта замена позволяет применить теорию КЗ линии и сразу же построить кривые распределения напряжения и тока в линии, нагруженной на индуктивность. В рассматриваемой линии возникают стоячие волны. Этот режим отличается от режима КЗ замыкания тем, что ближайший узел и пучность сдвинуты от конца линии на некоторое расстояние
. Заменим индуктивность Lн отрезком КЗ линии . Эта замена позволяет применить теорию КЗ линии и сразу же построить кривые распределения напряжения и тока в линии, нагруженной на индуктивность. В рассматриваемой линии возникают стоячие волны. Этот режим отличается от режима КЗ замыкания тем, что ближайший узел и пучность сдвинуты от конца линии на некоторое расстояние
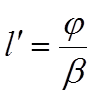
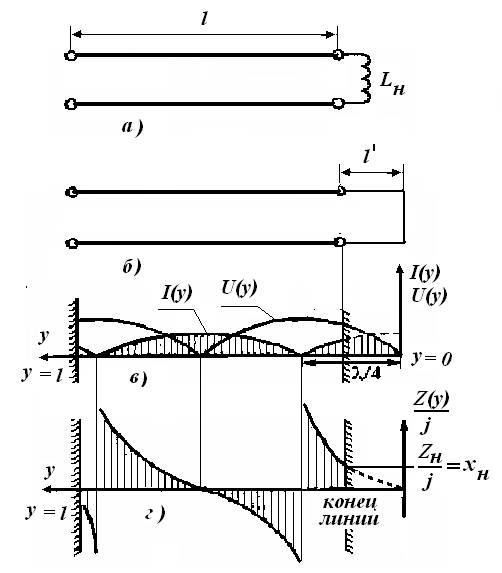
Следовательно, индуктивность в конце линии создает эффект удлинения линии доводя режим работы ее до режима КЗ.
В случае, когда линия нагружена на емкость 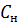 с сопротивлением
с сопротивлением 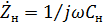 , можно заменить эту емкость отрезком разомкнутой линии длиной
, можно заменить эту емкость отрезком разомкнутой линии длиной 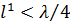 , входное сопротивление которого равняется заданному
, входное сопротивление которого равняется заданному 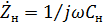 . Очевидно, и в этом случае в линии возникают стоячие волны.
. Очевидно, и в этом случае в линии возникают стоячие волны.
Режим смешанных волн
Режим смешанных волн наблюдается в линии, если нагрузка
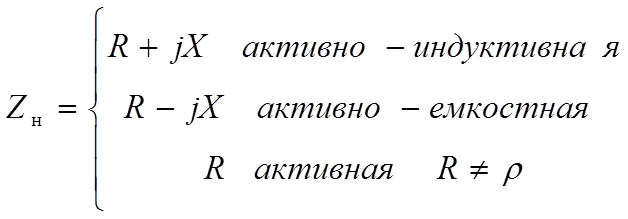
Включение линии на резистивное сопротивление, не равное волновому.
Положим для определенности, что сопротивление нагрузки 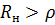 , и рассмотрим распространение по линии волны напряжения.
, и рассмотрим распространение по линии волны напряжения.
Падающая волна не вся поглощается нагрузкой, часть ее отражается обратно в линию. Амплитуда отраженной волны меньше амплитуды падающей волны, поэтому падающую волну можно представить в виде суммы двух волн. Одна из них, равная по амплитуде отраженной волне, взаимодействуя сней, образует стоячую волну. Оставшаяся падающая волна является бегущей. Таким образом, в линии возникает смешанная волна, состоящая из бегущей и падающей волн. Данный режим работы называется режимом смешанных волн.
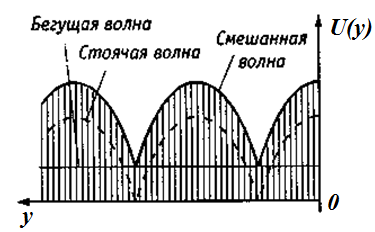
На рисунке показано распределение по длине линии, модуля комплексной амплитуды напряжения. В линии будут отсутствовать узлы и пучности, а будут наблюдаться минимумы и максимумы амплитуды волн.
Решения уравнений передачи для режима смешанных волн имют вид
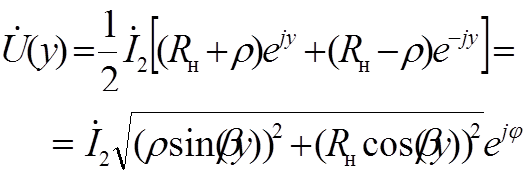
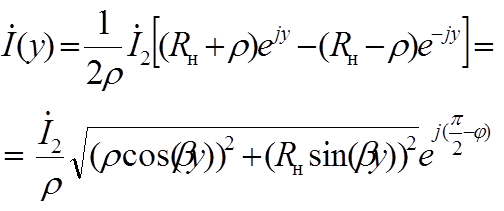
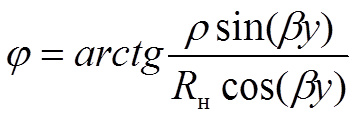
Распределение по длине линии амплитуды напряжения и тока в режиме смешанных волн
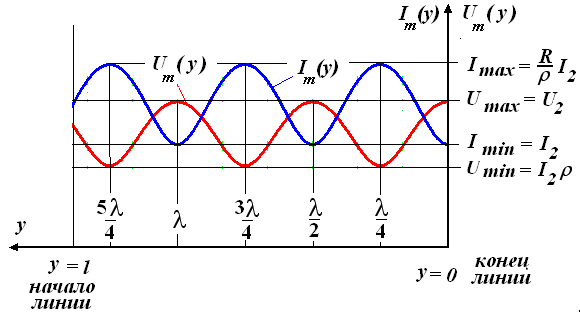
Чтобы оценить близость данного режима к режиму бегущей волны, вводят коэффициент бегущей волны:
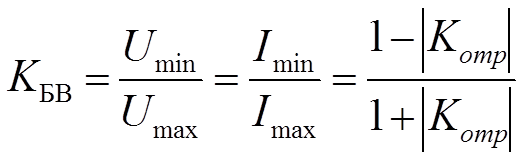
Величина 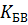 изменяется в пределах от 0 до 1. При
изменяется в пределах от 0 до 1. При 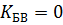 в линии имеет место стоячая волна, при
в линии имеет место стоячая волна, при 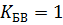 – бегущая волна.
– бегущая волна.
Коэффициент бегущей волны можно выразить через волновое сопротивление и сопротивление нагрузки.
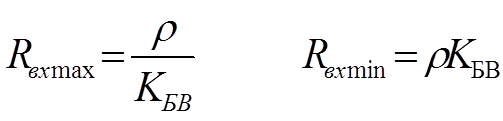
Входное сопротивление линии определяется по формуле
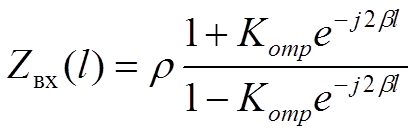
Часто используют обратную величину обратную 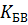 , которую называют коэффициентом стоячей волны.
, которую называют коэффициентом стоячей волны.
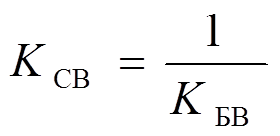
Применение линий без потерь в высокочастотной технике.
Экспериментальное определение первичных(погонных) параметров длинных линий
Из опытов холостого хода (Zн=¥)и короткого замыкания (Zн=0)можно получить, рассматривая линию как частный случай симметричного четырехполюсника:
- волновое сопротивление линии
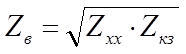
- характеристическая постоянная передачи линии
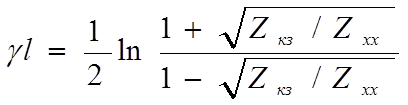
Тогда можно записать
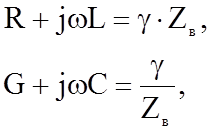
Откуда следует
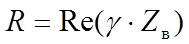
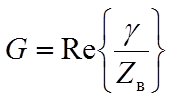
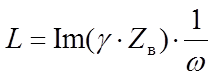
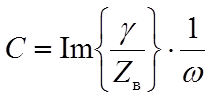
Использование отрезков длинных линий в военной технике связи
Металлический изолятор
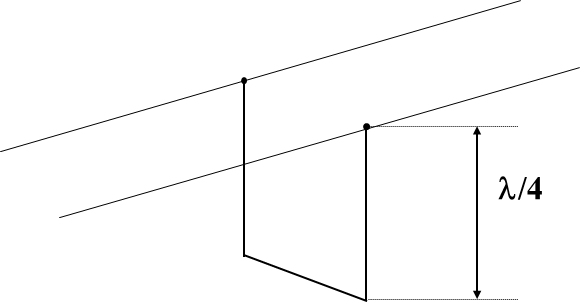
В режиме к.з 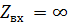 . С учетом потерь в линии
. С учетом потерь в линии
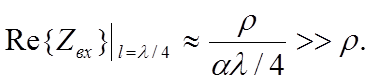
Отрезки линий без потерь как реактивное сопротивление
входное сопротивление линии без потерь в режмие короткого замыкания
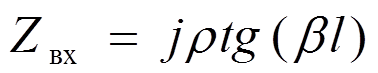
входное сопротивление линии без потерь в режиме холостого хода
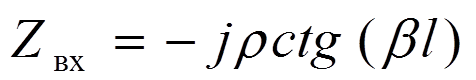
Такие отрезки можно использовать в микроэлектронике (например, в печатных платах).
Отрезок длинной линии без потерь длиной 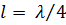 в режиме К.З., как параллельный колебательный контур
в режиме К.З., как параллельный колебательный контур
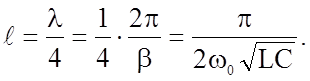
Отсюда следует, что резонансная частота колебательного контура
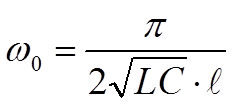
Полоса пропускания
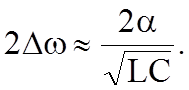
Добротность контура
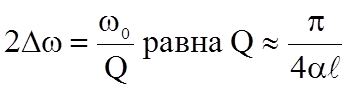
Для реальных отрезков длинных линий добротность может достигать значений 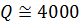 . Для сравнения добротность низкочастотных колебательных контуров, выполненных на катушках индуктивностей и конденсаторах составляет порядка 400.
. Для сравнения добротность низкочастотных колебательных контуров, выполненных на катушках индуктивностей и конденсаторах составляет порядка 400.
Резонансное сопротивление контура на отрезке длинной линии
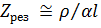 .
.
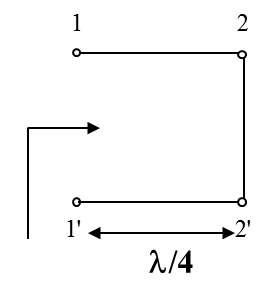
Трансформатор сопротивлений
при длине l =l/4 входное сопротивление длинной линии
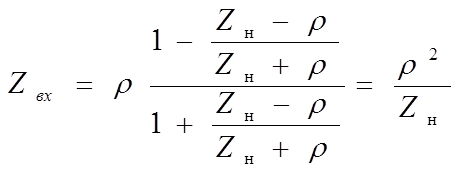
Согласование высокочастотных кабелей с различными волновыми сопротивлениями
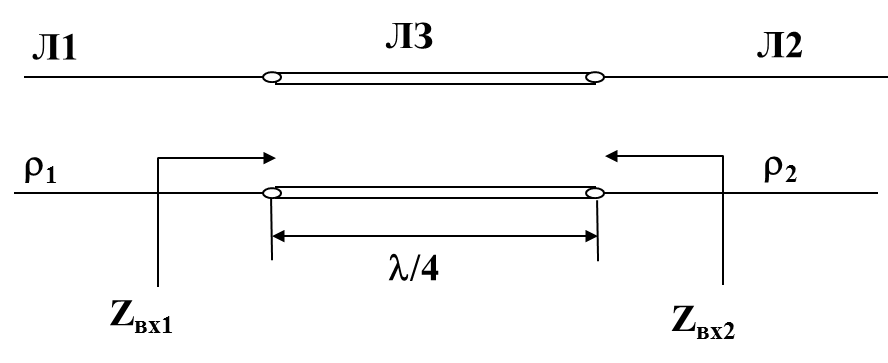
Как известно, наиболее эффективный режим работы длинных линий , как и четырехполюсников, это режим согласованной нагрузки, который наступает при подключении в конце линии нагрузки равной волновому сопротивлению линии. Если обеспечить сопротивление Zвх1 равным волновому сопротивлению Л1, то эта линия будет работать в согласованном режиме. Аналогично, и Л2 с нагрузкой равной Zвх2 равной 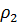 будет согласована по нагрузке. Для обеспечения этих режимов необходимо, чтобы согласующая линия Л3 имела воловое сопротивление
будет согласована по нагрузке. Для обеспечения этих режимов необходимо, чтобы согласующая линия Л3 имела воловое сопротивление 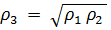 . В этом случае
. В этом случае
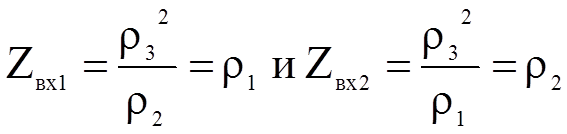
Переходные процессы. Общие сведения. Исходные уравнения и их решение.
При включении длинной линии без потерь на источник напряжения изменяющийся во времени по произвольному закону необходимо решить систему дифференциальных уравнений в частных производных называемых волновыми (телеграфными) уравнениями. В курсе математической физике это уравнения эллиптического типа.
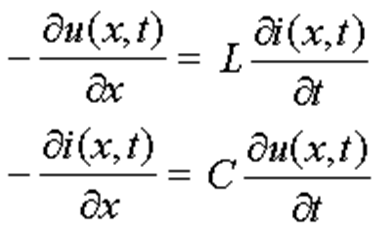
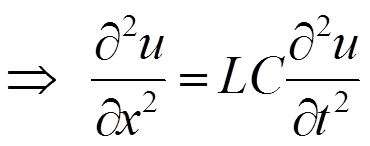
Решение волнового уравнения для линии без потерь имеет вид суммы двух слагаемых, представляющих падающую и отраженную волну
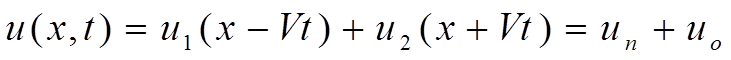
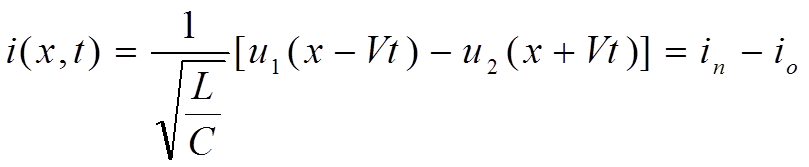
где
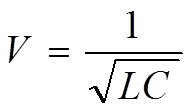
скорость распространения волн
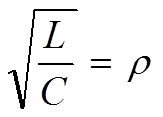
волновое сопротивление линии.
Вид функций uп , uo сложный и получить его аналитическое выражение затруднительно.
Проще найти решение для u(x,t) пользуясь понятием коэффициента отражения от конца и начала линии.
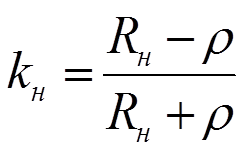
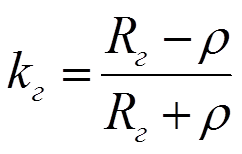
Идея упрощенного метода расчета переходных процессов в длинных линиях заключается в наложени волн в переходных процессах при включении длинной линии без потерь на ступеньки постоянных напряжений, которые приближенно описывают закон изменения входного напряжения источника (генератора).
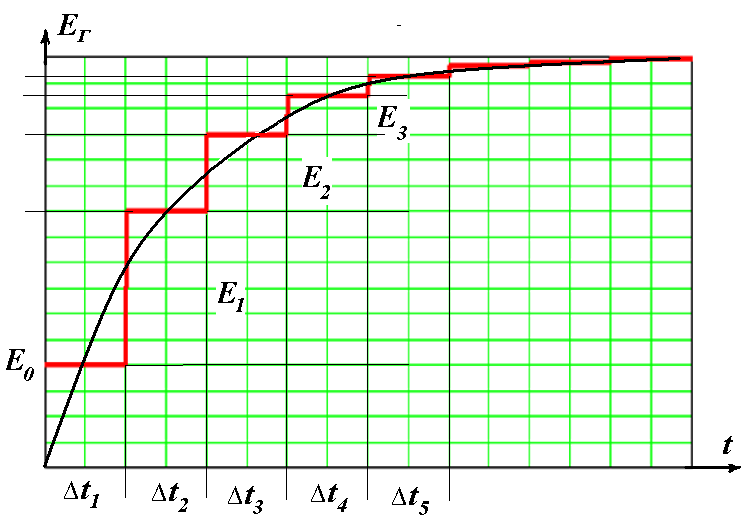
В результате наложения
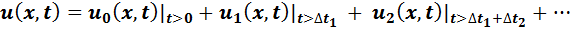
Переходные напряжения u0(x,t) , u0(x,t) , u0(x,t) , … есть следствие включения длинной линии без потерь на постоянные напряжения, соответствующие ступенькам, аппроксимирующим график входного напряжения генератора. При окончательном суммировании этих переходных напряжений от каждой из ступенек следует учесть сдвиг по времени при учете каждого из переходных напряжений.
Волны с прямоугольным фронтом
Таким образом мы пришли к необходимости уметь расчитывать переходной процесс при включении длинной линии без потерь на постоянное напряжение.
В момент включения линии на постоянное напряжение появляется падающая волна. На интервале времени ( τ ) от момента коммутации до момента прихода волны к концу линии (к нагрузке) в линии наблюдается режим бегущей волны. При таком режиме входное сопротивление линии равно волновому сопротивлению линии. Схема замещения соответствующая такому режиму имеет вид
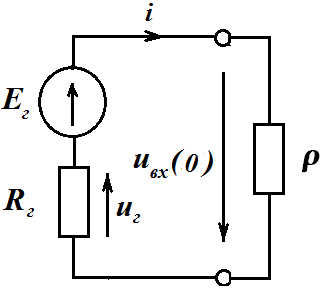
Из расчета схемы следует
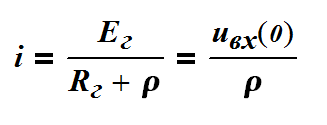
По сопротивлению генератора, волновому сопротвлению линии и постоянному напряжению источника (генератора) находится входное нпряжение линии в момент коммутации.
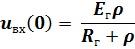
После многократных отражений волны в линии от нагрузки и от генератора в переходном режиме в линии установится режим постоянного тока, что соответствует следующей схеме замещения.
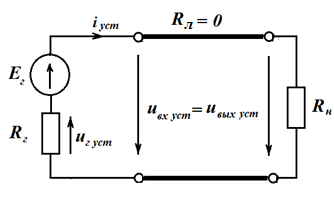
Из схемы следует
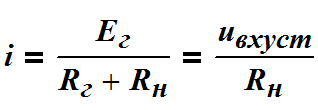
Полученное выражение позволяет вычислить входное и выходное напряжения линии в установившемся режиме .
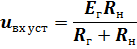
Коэффициенты отражения от источника и нагрузки определяются по значениям сопротивлений нагрузки, генератора и волновому сопротвлению линии.
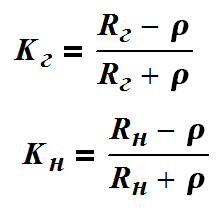
Значения напряжений в начале и конце линии в моменты очередных отражений от генератора и нагрузки могут быть рассчитаны в соответствии с теорией с помощью коэффициентов отражений по рекурентным формулам.
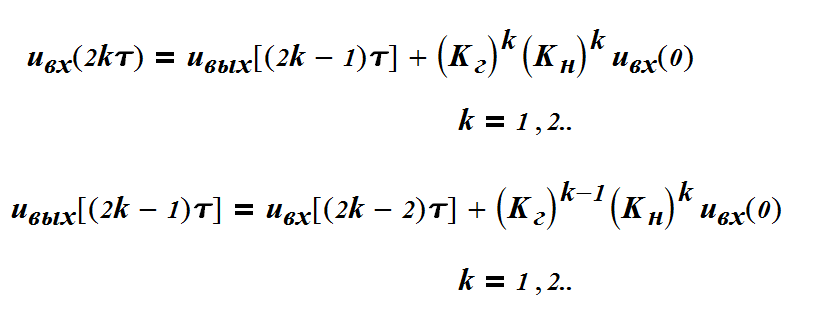
При этом
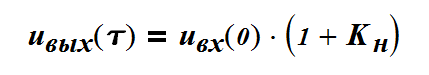
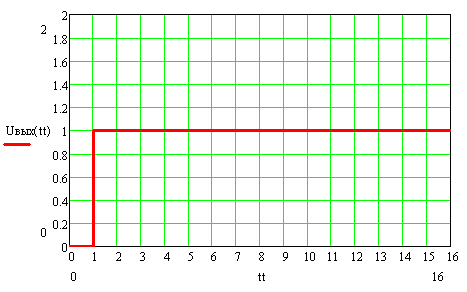
Ниже приведены графики переходных напряжений на входе и выходе линии без потерь при различных граничных условиях в конце линии.
Режим холостого хода ( Rн=∞ , Rг=3ρ, Ег=4 В)
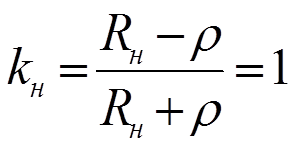
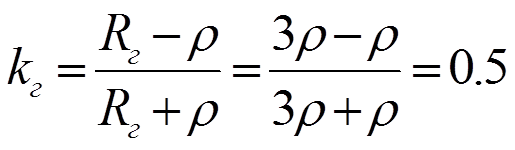
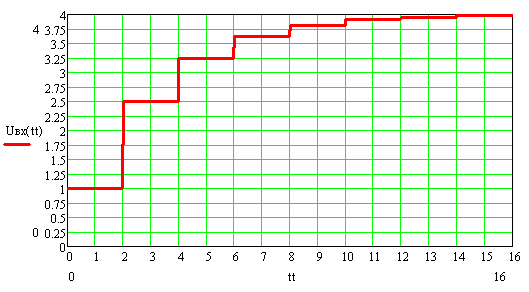
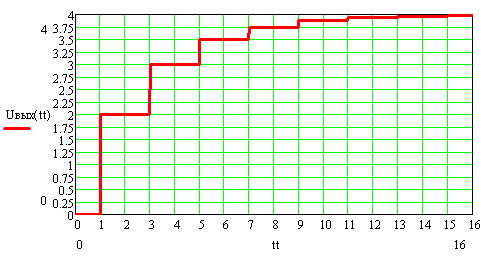
Режим короткого замыкания ( Rн=0 , Rг=3ρ, Ег=4 В)
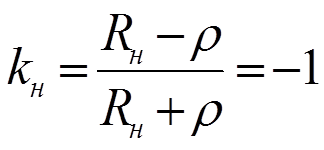
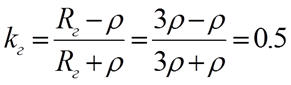
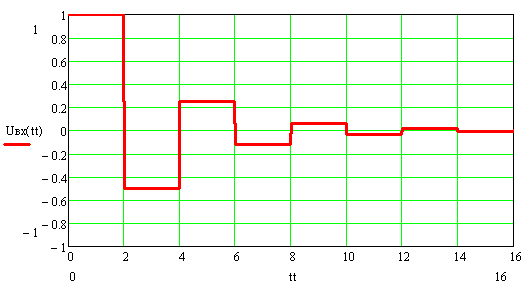
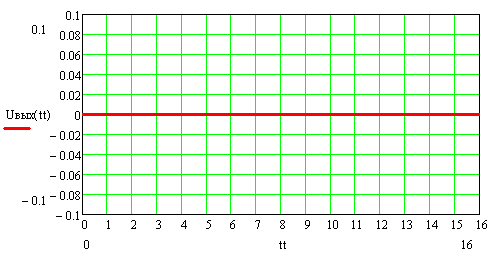
Сопротивление нагрузки больше волнового ( Rн=3ρ , Rг=3ρ, Ег=4 В)
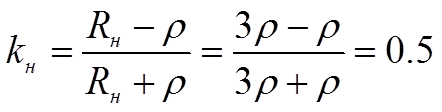
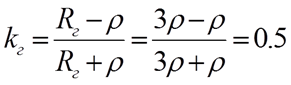
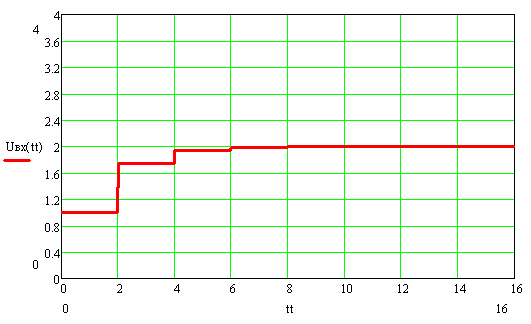
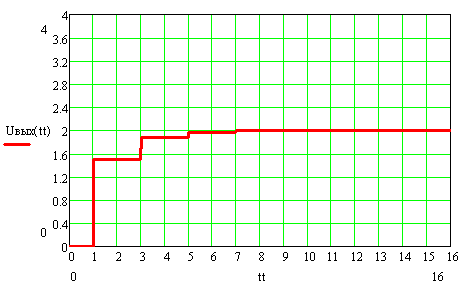
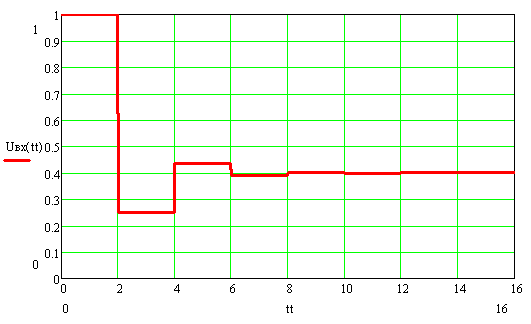
Сопротивление нагрузки меньше волнового ( Rн=1/3ρ , Rг=3ρ, Ег=4 В)
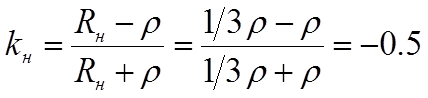
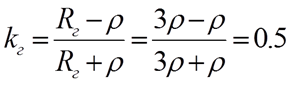
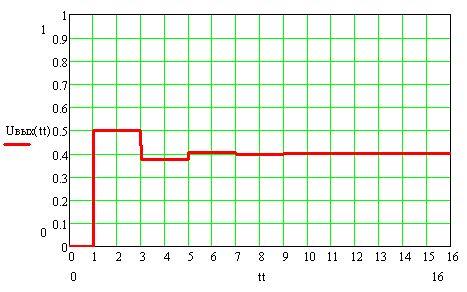
Сопротивление нагрузки равно волновому ( Rн=ρ , Rг=3ρ, Ег=4 В)
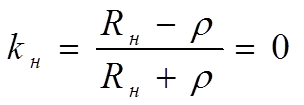
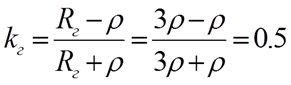
Дата добавления: 2020-03-21; просмотров: 1341;











