Интерференционные полосы в плоскопараллельной пластине

Рассмотрим прозрачную плоскопараллельную пластинку, освещаемую точечным источником S (рис.8.18).

Рис. 8.18 Интерференция в плоскопараллельной пластине

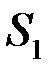Очевидно, для любой точки P всегда можно найти два луча, отразившиеся от разных поверхностей пластины и приходящие в эту точку из источников и 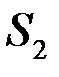, являющихся изображениями источника 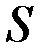. Интерферируя, эти лучи образуют нелокализованную интерференционную картину. Из симметрии ясно, что эти картины имеют вид концентрических колец с осью SN, нормальной к пластине, и при любом положении P полосы перпендикулярны плоскости SNP. Как уже отмечалось, в этом случае увеличение размеров источника S в направлении, ортогональном плоскости SNP практически не влияет на видимость интерференционной картины, а в направлении параллельном плоскости SNP резко ухудшает её видимость. Можно, однако, показать, что в одном случае видимость картины практически не зависит от размеров источника. Это случай, когда источник S находится в бесконечности. На пластину при этом лучи падают под одним и тем же углом 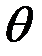и, следовательно, отразившиеся от поверхности пластины лучи будут также параллельны, т.е. интерферировать в бесконечности (рис. 8.19). Поэтому, говорят, что интерференционная картина локализована в бесконечности.

Рис. 8.19 Интерференционные кольца равного наклона, локализованные в бесконечности

Оптическая разность хода между лучами равна:

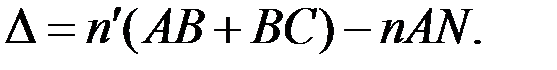
Если толщина пластины 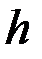, а углы падения и преломления и 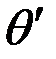соответственно, то ; .

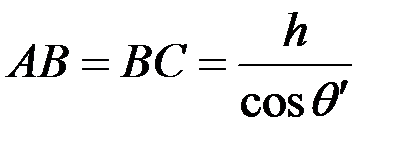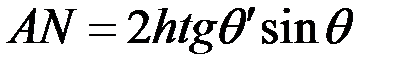Кроме того, по закону преломления

,

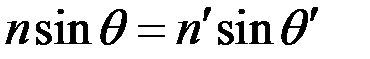следовательно

.

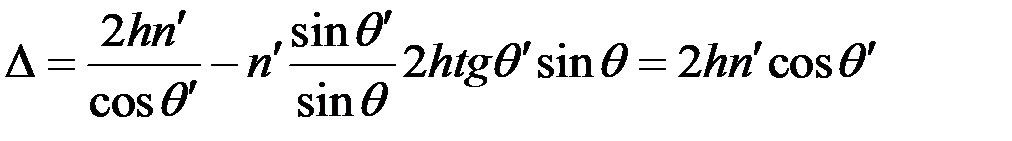Соответствующая разность фаз равна

.

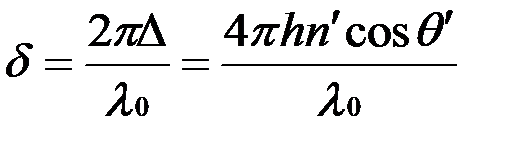Следует также учитывать изменение разности фаз на 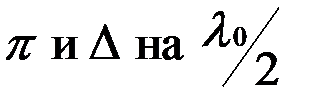, которое, согласно формулам Френеля, происходит при отражении от более плотной оптической среды. В частности, при 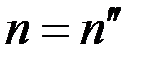получаем:

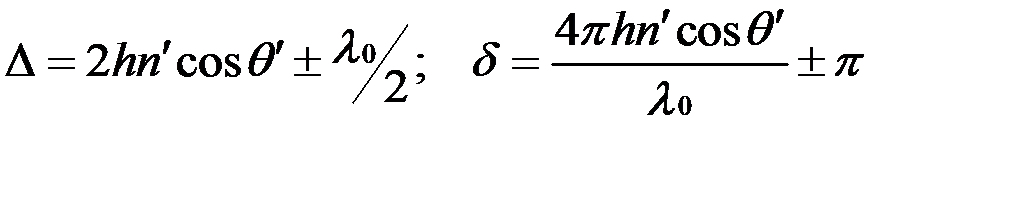, (8.17)

или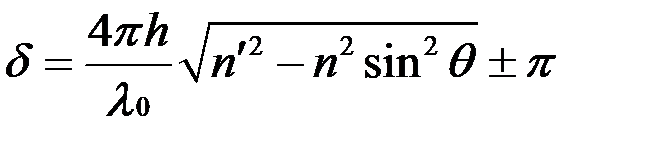

Можно показать, что выражения (8.17) имеют место во всех случаях, когда изменение показателей преломления сред 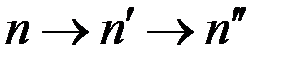имеет немонотонный характер, в противном случае слагаемые 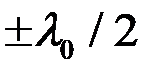и 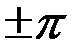отсутствуют.

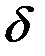Возникающая интерференционная картина может наблюдаться в бесконечности или в фокальной плоскости линзы Л. Поскольку значения величин и не зависят от положения источника S, то это значит, что при использовании протяженного источника полосы будут такими же чёткими, как и при точечном источнике, другими словами: размеры источника не оказывают большого влияния на контраст интерференционной картины, как это имело место в методе деления волнового фронта. В этом состоит основное преимущество локализованной интерференционной картины в методе деления амплитуды.

Условие постоянной интенсивности в интерференционной полосе имеет вид:

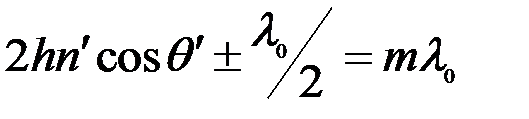. (8.18)

При этом значениям m=0, 1, 2…. соответствует максимум, а значениям m=1/2, 3/2, 5/2 …- минимум интенсивности. Каждая полоса характеризуется только углом наблюдения 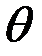(значит 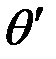) и, следовательно, углом падения. Поэтому такие полосы называют кольцами равного наклона. При нормальном падении 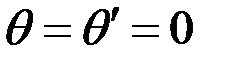, порядок интерференции 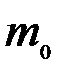в центре будет максимален и определяться из условия:

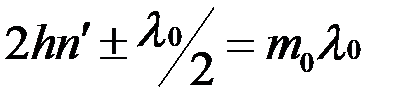, (8.19)

откуда

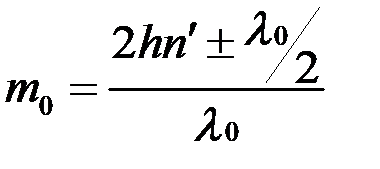. (8.20)

Обычно (8.20) не дает целого значения 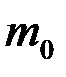, поэтому его можно представить в ви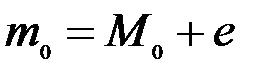де: , где 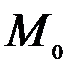- целая часть 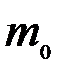, e – дробная часть .

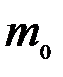Из (8.18) для 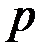-го максимума запишем:

,

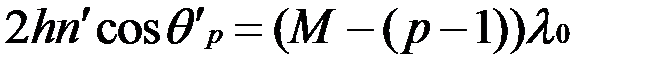откуда с учетом (8.19) получаем:

.

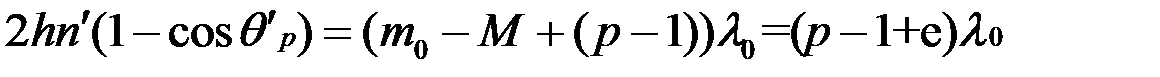Если 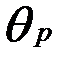мало, то 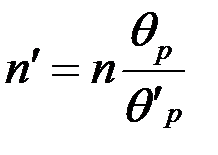; 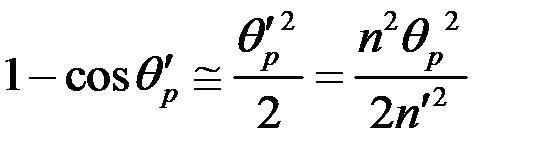и, следовательно,

,

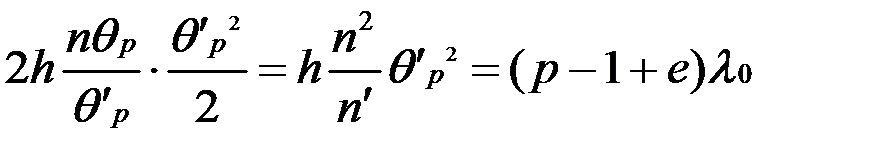откуда

.

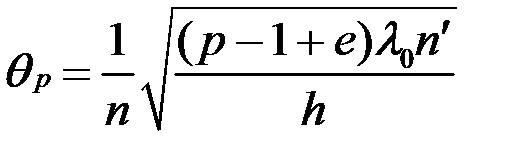Т.е. угловые радиусы колец пропорциональны квадратному корню из положительных целых чисел.

Рис. 8.20 Интерференция в проходящем свете

Аналогичным образом можно рассмотреть интерференцию в проходящем свете (рис.8.20). В этом случае разность хода и разность фаз определяются аналогичными выражениями:

; .

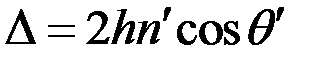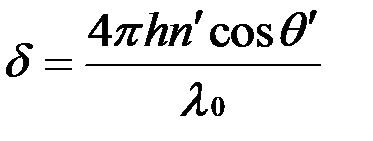При 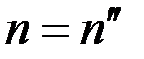дополнительные слагаемые ( 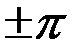) и ( 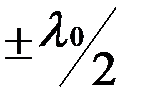) отсутствуют, т.к. оба отражения происходят в одинаковых условиях (либо от более плотной, либо от менее плотной среды). Интерференционная картина в этом случае также локализована в бесконечности, однако контраст будет заметно ниже, чем в предыдущем случае (см. решение задачи 3).

Наши рассуждения, вообще говоря, не совсем строги, т.к. мы не учитывали многократных отражений на поверхностях, однако, если коэффициент отражения 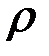мал, то влиянием других отражений можно пренебречь.