Влияние сопротивления деформации материала полосы на контактные напряжения

Как указано в п. 6.1, третье уравнение системы, необходимой для получения расчетных формул контактных напряжений, характеризует напряженно-деформированное состояние материала полосы.

На пластических участках очага деформации это – уравнение (или условие) пластичности, которое чаще всего выражают в виде:

σ₁- σ₃ = 1,15σ_Ф = 2τ_S, (6.2)

где σ₁, σ₃ – максимальное и минимальное главные нормальные напряжения, действующие в полосе в процессе прокатки;

σ_Ф, τ_S – значения сопротивления пластической деформации (фактического сопротивления простому сжатию) и сопротивления чистому сдвигу материала полосы.

На упругих участках очага деформации напряженно-деформированное состояние материала полосы соответствует не условию (6.2), а уравнению упругой деформации:

σ₁- σ₃ = 1,15σ (ε_hx); (6.3)

где σ(ε_hx) – напряжение, возникающее в образце, изготовленном из материала полосы, когда его подвергают при механических испытаниях упругому сжатию с такой же относительной деформацией ε_hx, как и прокатываемую полосу. При этом, как и в очаге деформации, образец сжимают от значения ε_hx=0 до значения, предельного для упругой деформации:

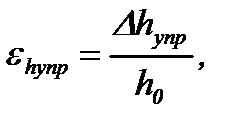(6.4)

где h₀ – первоначальная высота образца, равная толщине полосы на входе в очаг деформации;

Δh_упр – обжатие, равное изменению толщины в конце упругого участка очага деформации, когда сжимающее напряжение в образце достигло значения σ_Ф, при котором начинается пластическая деформация:

σ (ε_hупр) = σ_Ф. (6.5)

Напряжение s(ε_hx), по аналогии с величиной σ_Ф , может быть названо сопротивлением упругой деформации.

При упругом сжатии образца действует закон Гука:

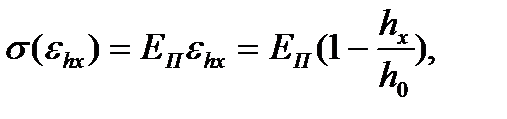(6.6)

где E_П – модуль упругости материала полосы;

h_x –текущая высота сжимаемого образца, равная текущей толщине полосы на упругом участке очага деформации.

Подставив выражение (6.6) в уравнение (6.3), получим уравнения напряженно-деформированного состояния полосы на упругих участках очага деформации:

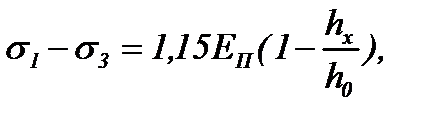(6.7)

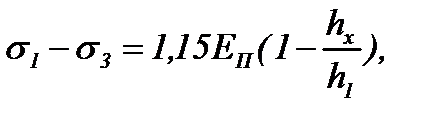(6.8)

Как видно из уравнений (6.2), (6.7) и (6.8), они связывают главные напряжения, действующие в полосе во время прокатки, с механическими характеристиками материала полосы σ_Ф, τ_S, E_п.

Таким образом, указанные механические характеристики материала полосы оказывают большое влияние на величину контактных напряжений в очаге деформации, а, следовательно, и на остальные энергосиловые параметры процесса прокатки.

Поэтому, прежде чем начинать энергосиловой расчет, необходимо найти справочные данные о величинах сопротивления пластической деформации и модуля упругости материала полосы. Подробно этот вопрос рассмотрен в главе 2, где в п.2.4. приведены формулы для определения σ_Ф, σ_0,2 и τ_S, наиболее часто используемые на практике, и указана справочная литература, в которой имеются значения этих величин для различных сталей и сплавов.