Интерферометр Фабри-Перо

На практике многолучевая интерференция реализуется чаще всего на интерферометре Фабри-Перо (рис. 8.32). Он представляет собой две стеклянные или кварцевые пластинки P₁ и P₂ с плоскими поверхностями. Внутренние рабочие поверхности пластин, покрытые частично прозрачными элементами с высоким коэффициентом отражения ρ, параллельны, и образуют плоскопараллельную пластину. Сами пластины слегка клиновидны для исключения влияния паразитных отражений от нерабочих поверхностей.

Рис. 8.32. Схема интерферометра Фабри-Перо

Пластины разделяют кольцом D с тремя выступами на торцах (инвар, кварц), к которым пластины поджимают пружинками. Такой интерферометр называют часто эталоном Фабри-Перо. Интерферометр освещается параллельным пучком света от источника, находящегося в передней фокальной плоскости F₁ линзы Л₁. Таким образом, в фокальной плоскости линзы Л₂ появится система очень резких концентрических колец, порядок которых убывает от центра к краю. Максимальный порядок m₀ в центре, в общем случае, также нецелое число, и если его представить в виде

,

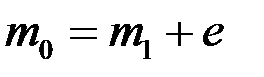где 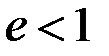– дробная часть порядка, то, как было показано, угловой размер p-го светового кольца

,

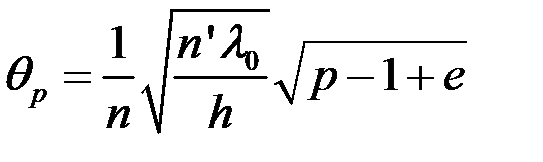и, следовательно, линейный радиус его в фокальной плоскости линзы Л₂ с фокусным расстоянием 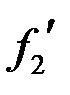равен

.

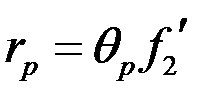Наиболее широкое применение эталон Фабри-Перо нашел при изучении тонкой структуры спектральных линий. Теоретически, информация о тонкой структуре линии содержится в распределении интенсивности в одном из максимумов, зная которое, можно в принципе определить тонкую структуру спектральной линии.

Рис. 8.33. Предельное разрешение двух спектральных линий в интерферометре Фабри-Перо

Мы рассмотрим сейчас частный случай, когда спектр излучения представляет собой две монохроматические компоненты с длинами волн 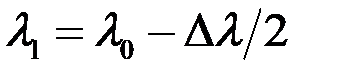и 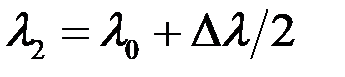, имеющие одинаковые интенсивности. Представим себе, что величина Δλ постепенно возрастает от нуля, и, в конце концов, наличие двух компонент в излучении будет замечено, поскольку в интерференционной картине появятся две смещенные друг относительно друга системы максимумов. Считается, что, согласно критерию Релея, наличие двух компонент будет установлено, если в суммарном распределении интенсивности возникает перепад, равный 0.2 от максимального (рис. 8.33). Это произойдет, если разность фаз 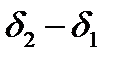максимумов одного и того же порядка этих длин волн будет равна некоторому значению 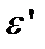, незначительно отличающемуся от полуширины линии 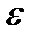. Запишем условие максимума для средней длины волны

,

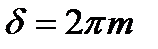где

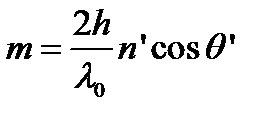, (8.29)

и потребуем, чтобы дифференциал 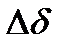был равен 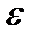, т.е.

.

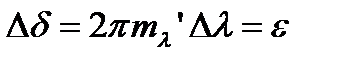Тогда с учетом (8.29) с точностью до знака получаем выражение:

,

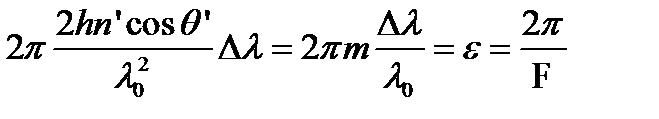из которого найдем условие предельного разрешения:

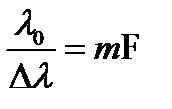. (8.30)

Величина 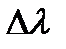, определяемая (8.30) в спектроскопии называется спектральным пределом разрешения, а отношение 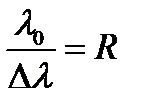– разрешающей способностью. Известно (глава 7), что разрешающая способность спектральных приборов с дифракционными решетками, имеющими число штрихов 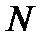и работающими в 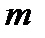-ом порядке

,

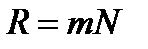поэтому по аналогии с (8.30) величину 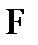часто называют эффективным числом интерферирующих пучков.

Интерферометр Фабри-Перо обладает наивысшей разрешающей способностью ( 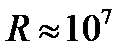) по сравнению с другими спектральными приборами (для сравнения у лучших дифракционных спектральных приборов 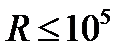). При изучении тонкой структуры спектральной линии часто требуется обеспечить заданное целое число m в пределах p-го кольца для разных значений 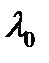из рабочего спектрального диапазона. Для этого, в соответствии с (8.29), изменяют либо угол 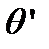(наклоном эталона), либо показатель преломления 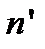(заполнением рабочей области эталона газом с известным показателем преломления), либо величину 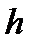(применением кольца из пьезоэлектрического материала).

Разновидностями интерферометра Фабри-Перо являются оптические резонаторы лазеров, активная среда которых располагается между зеркалами. Для волн 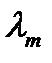, распространяющихся вдоль оси резонатора ( 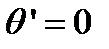) при 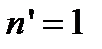, он обладает высоким пропусканием при условии (8.5), т.е. при

,

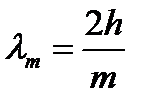где m – целое число.

Соответствующие частоты

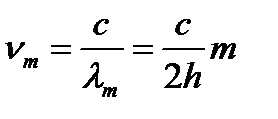
образуют эквидистантный спектр частот резонатора, с расстоянием между частотами 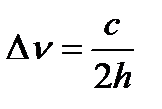. Резонатор Фабри-Перо с такими зеркалами чувствителен к деформации и перекосам зеркал, что ограничивает их применению. Этого недостатка лишены оптические резонаторы со сферическими зеркалами.

Задачи и примеры

Задача1. Определить контраст интерференционной картины, если интенсивности интерферирующих пучков различаются в 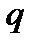раз. Провести расчет для .

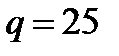Решение.Пусть 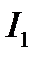и - и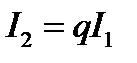нтенсивности первого и второго пучков, тогда общая интенсивность при интерференции равна

.

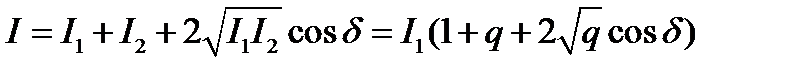Следовательно, максимальная и минимальная интенсивности равны

, .

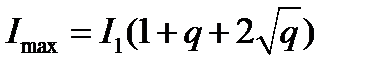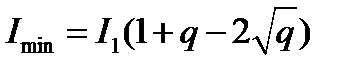По определению контраста находим

.

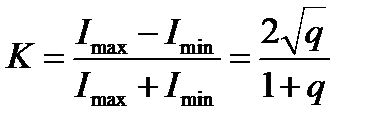Для 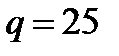получаем .

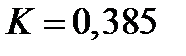Т.е. контраст достаточно высокий.

Задача2. Определить контраст интерференционной картины, образованной пучками равной интенсивности 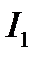и наблюдаемой на фоне постоянной некогерентной засветки с интенсивностью 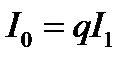. Провести расчет для .

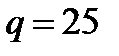Решение.Интенсивность интерференционной картины при 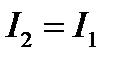, равна

.

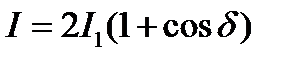Максимальная и минимальная интенсивности при наблюдении на фоне засветки 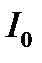равны

, .

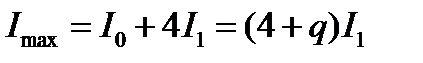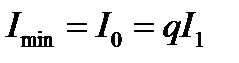Наблюдаемый контраст равен

.

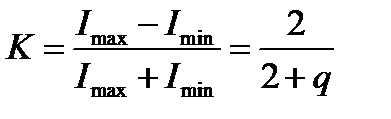Для 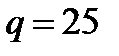получаем 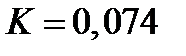- значительно меньше, чем в задаче 1.

Постоянная засветка сильно снижает контраст.

Задача3.Определить, во сколько раз контраст интерференционной картины в плоскопараллельной пластине с показателем преломления 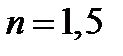в отраженном свете больше, чем тот же контраст в проходящем свете.

Решение.Коэффициент отражения одной поверхности пластины определим по формуле Френеля при нормальном падении света

.

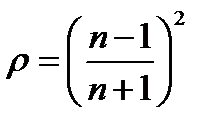При 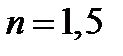он будет равен 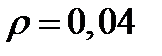. Поскольку коэффициент отражения мал, то влиянием многократных отражений можно пренебречь. Будем также пренебрегать поглощением света в пластине и изменением интенсивности при прохождении через границу раздела. Тогда интенсивности пучков, отраженных от двух плоскостей пластины, равны

, ,

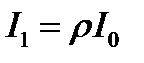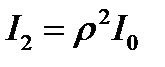где 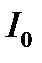- интенсивность падающего света.

Отношение интенсивностей

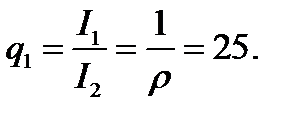
Интенсивности двух интерферирующих пучков в прошедшем свете

, ,

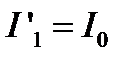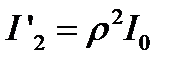и, следовательно, отношение этих интенсивностей

.

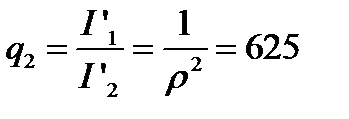Для определения контраста используем решение задачи 1, откуда получаем

, .

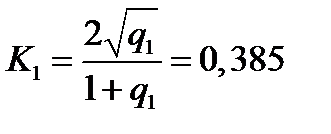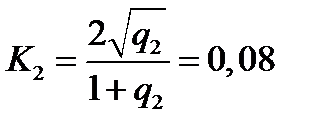Отсюда следует, что 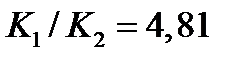, т.е. контраст интерференционной картины в отраженном свете выше того же контраста в проходящем свете почти в 5 раз.

Задача 4. Рассчитать параметры просветляющей пленки для стеклянной пластины с показателем преломления 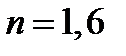, обеспечивающей нулевой коэффициент отражения на длине волны 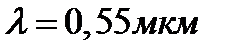. Какой цвет будет иметь поверхность просветленной пластины при освещении её белым цветом.

Решение.Расчет параметров пленки заключается в нахождении её толщины 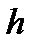и показателя преломления 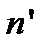. Искомые значения 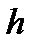и 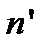должны обеспечить нулевой минимум при интерференции в пленке в отраженном свете. Как известно нулевой минимум при интерференции достигается при равенстве интенсивносте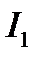й и 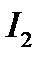интерферирующих пучков и при условии

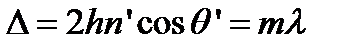, (1)

где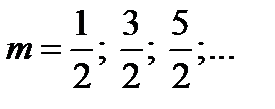

Расчет будем проводить для нормального падения света на пластину. Равенство интенсивностей обеспечивается одинаковым коэффициентом отражения от двух поверхностей пленки. По формуле Френеля получим

.

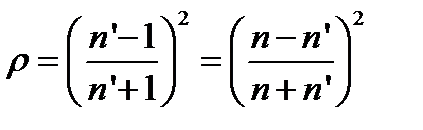Из последнего уравнения получаем

.

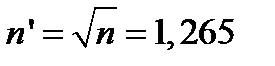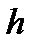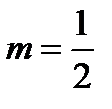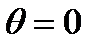Толщину найдем из (1) при и . Получаем

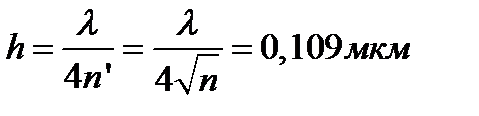
Найденные значения 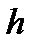и 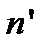обеспечивают нулевой коэффициент отражения от просветленной пластины на длине волны 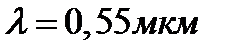. Для оценки цвета пластины при освещении её белым светом определим коэффициенты отражения 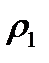и 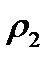пленки на длинах волн 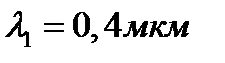и 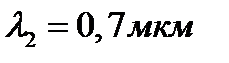соответственно.

,

,

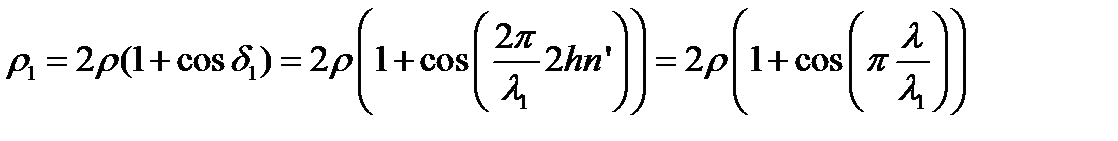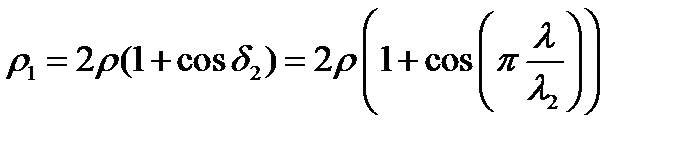После вычислений получаем 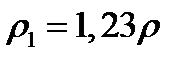; 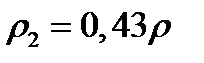. Коэффициент отражения поверхности пленки 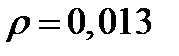, поэтому ; .

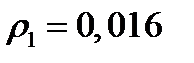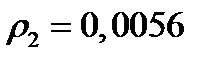Цвета получающиеся в результате смешивания сине-фиолетовых и оранжевых цветов называются пурпурными, поэтому пластина в отраженном свете будет окрашена в пурпурный цвет с преобладанием синего. Коэффициент отражения непросветленной пластины

.

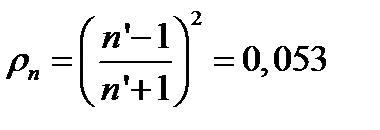Сравнив получившееся значениекоэффициента отражения пластины с 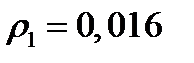и 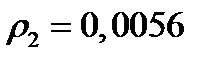видим, что просветляющая пленка значительно уменьшает коэффициент отражения во всей видимой области спектра.

Задача 5. Плоскопараллельную пластину поочередно кладут на две поверхности двояковыпуклой тонкой стеклянной линзы. При этом радиус двадцатого темного кольца (m=20) в свете длины волны λ=589 нм в одном случае равен r₁=2 мм, а в другом − r₂=4 мм. Определить фокусное расстояние f’ линзы, если показатель преломления стекла n=1,5.

Решение. Для двух случаев можно записать:

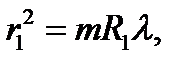
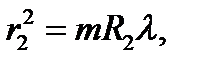
где R₁ и R₂ − радиусы поверхностей линзы.

Искомое фокусное расстояние линзы определим из соотношения

.

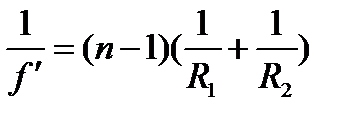Отсюда

.

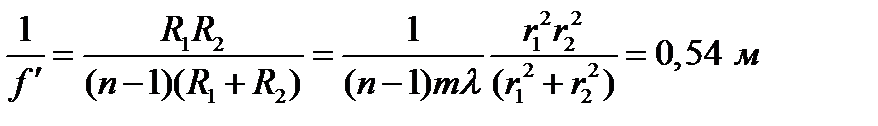Задача 6. В опыте Винера длина волны λ излучения и ширина спектра Δλ точечного источника измеряется путем фотографирования пучностей стоячих волн на фотопластинку, установленную под углом 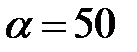угл. мин. к плоскому зеркалу. Определить λ и Δλ, если после проявления фотопластинки, на ней оказались зарегистрированными N=1200 интерференционных полос шириной b=0.02 мм с постоянно уменьшающимся контрастом.

Решение. Расстояние между соседними пучностями в стоячей волне

.

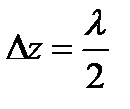Ввиду малости угла α расстояние между полосами на фотопластинке можно определить следующим образом:

,

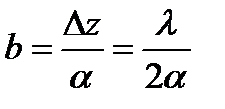откуда

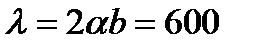нм .

Для оценки ширины полосы Δλ отметим, что полосы становятся неразличимыми, когда пучность номера N для длины волны λ+Δλ совпадает с пучностью номера N+1 для длины волны λ, т. е.

,

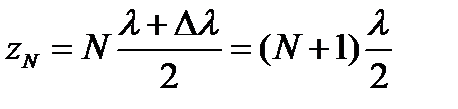отсюда получаем:

нм .

Задача 7. Эталон Фабри-Перо представляет собой стеклянную пластинку (n=1.5) с нанесенным на обе стороны отражающем покрытием ( 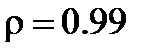). Толщина пластинки h=5 мм. Будут ли разрешаться таким эталоном две монохроматические линии одинаковой интенсивности, длины волн которых различаются на 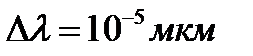, а средняя длина волны ?

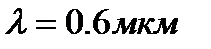Найти угол 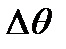между пятым и шестым максимумами интерференции в проходящем свете, считая, что нулевой максимум наблюдается в направлении нормали к поверхности эталона.

Решение. Для того чтобы указанные линии разрешались, необходимо, чтоб разрешающая способность эталона была равна:

.

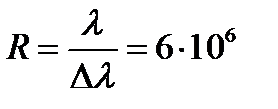Рассматриваемый эталон имеет разрешающую способность:

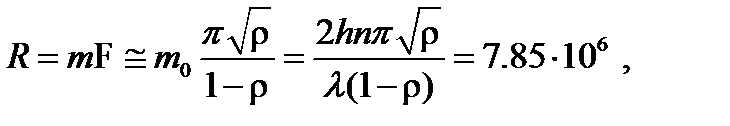
т. е. превышает требуемую. Следовательно, линии разрешаются.

Угловой размер p-ого максимума определяется выражением:

,

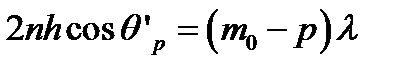где 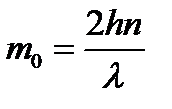- максимальный порядок интерференции при . 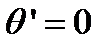Отсюда получаем выражение:

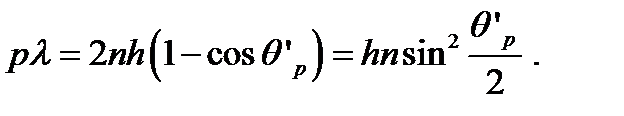
Последнее выражение с учетом малости углов 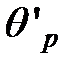преобразуем так:

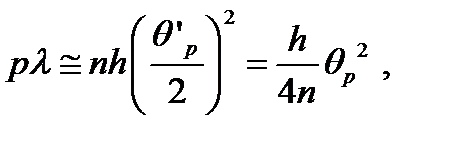
откуда получаем:

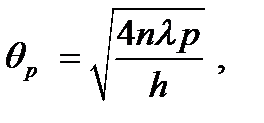
и, следовательно, искомый угол равен

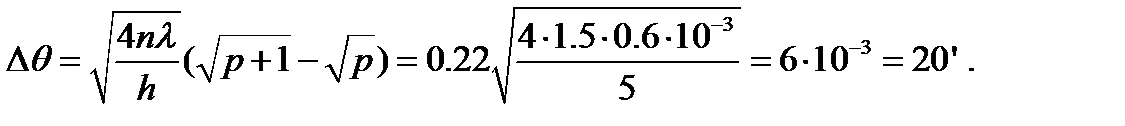
Вопросы для самоконтроля

1. Чем отличаются друг от друга методы деления волнового фронта и амплитуды?

2. Как определяется общая интенсивность при интерференции монохроматических волн?

3. Назовите известные способы реализации метода деления волнового фронта.

4. К чему приводят увеличение спектральной ширины и размеров источника излучения при интерференции?

5. Что такое стоячая волна, узлы и пучности стоячей волны?

6. Где локализованы интерференционные кольца равного наклона?

7. Где локализованы интерференционные полосы равной толщины?

8. Как реализуются кольца равного наклона и полосы равной толщины в интерферометре Майкельсона?

9. Чем отличается интерференционная картина при многолучевой интерференции от интерференционной картины при двулучевой интерференции?

10. Что такое резкость интерференционных полос при многолучевой интерференции?

11. Как устроен интерферометр Фабри – Перо?

12. Каким образом в интерферометре Фабри – Перо осуществляется изменение оптической разности хода между интерферирующими пучками?

13. Какие преимущества имеет интерферометр Фабри – Перо при использовании в качестве спектрального прибора?

14. Какие преимущества и недостатки имеет интерферометр Фабри – Перо при использовании в качестве резонатора лазера?