Ламинарный пограничный слой на плоской пластине
Продольно – обтекаемая ламинарным потоком пластина является одним из наиболее широко распространенных элементов поверхностей современных теплообменных аппаратов. Поэтому знание закономерностей протекания процессов теплообмена на пластине с точки зрения современной практики и теории теплообмена остается весьма актуальным. Нередко при разработке точных и приближенных аналитических методов решения различных задач теплообмена с целью первой их проверки обращаются к обтеканию плоской пластины, что еще раз подтверждает важность точного знания закономерностей ее теплообмена.
Рассмотрим обтекание пластины при ламинарном режиме. В этом случае уравнения неразрывности (1.1) и Навье - Стокса (1.2) примут вид:
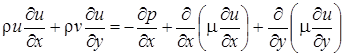 ; (2.1)
; (2.1)
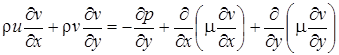 ; (2.2)
; (2.2)
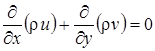 . (2.3)
. (2.3)
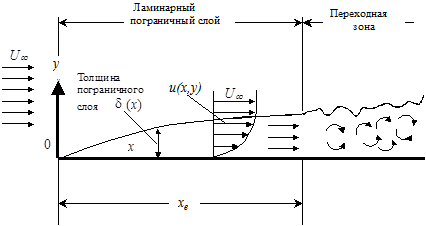 |
При обтекании пластины (рис. 2.1) реальной жидкостью на ее поверхности вследствие действия сил вязкости образуется область, именуемая пограничным слоем. За пределами этой области течение практически происходит без трения, т.е. оно подчиняется законам идеальной жидкости.
Рис. 2.1.Ламинарный пограничный слой на плоской пластине
Уравнением (2.2) можно пренебречь, поскольку силы, действующие в нормальном направлении к обтекаемой поверхности, значительно меньше сил, действующих в касательном направлении, а поперечный градиент давления мал.
Тогда уравнения (2.1) и (2.3) примут вид:
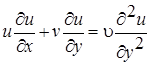 (2.4)
(2.4) 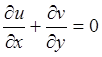 . (2.5)
. (2.5)
При решении данной задачи принимаются следующие граничные условия:
при у = 0; u = v = 0, (2.6)
при y ® ¥, u = U∞.
Введем вместо координаты у другую, безразмерную координату, разделив для этого у на d, т. е. положим
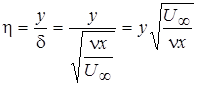 . (2.7)
. (2.7)
Далее введем функцию тока y(x, у). Примем, что
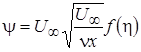 , (2.8)
, (2.8)
где f (η) есть безразмерная функция тока. Тогда
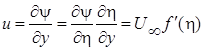 ;
;
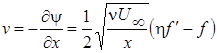 .
.
Подставив эти выражения в уравнение движения (2.4), получим для определения безразмерной функции тока f(h) уравнение
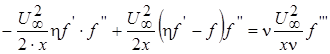 (2.9)
(2.9)
или, после упрощения 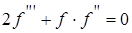 , (2.9а)
, (2.9а)
т.е. обыкновенное дифференциальное уравнение, с граничными условиями
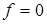 ,
, 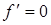 при
при 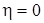 ,
,
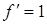 при
при 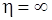 . (2.10)
. (2.10)
Подробное решение уравнения (2.9) при использовании численного метода приведено в работе [4].
Если принять, что толщина пограничного слоя равна расстоянию от пластины, на котором 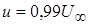 , то, используя данные численного решения уравнения (2.9) [4], ее можно выразить следующим уравнением:
, то, используя данные численного решения уравнения (2.9) [4], ее можно выразить следующим уравнением:
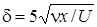 . (2.11)
. (2.11)
Из уравнения (2.11) следует, что пограничный слой с удалением от передней кромки пластины возрастает, подчиняясь закону 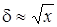 .
.
К числу очень важных гидродинамических характеристик обтекания пластины относятся местное и среднее сопротивления трения на поверхности пластины. Указанные сопротивления трения можно определить путем использования данных [1] и уравнения местного касательного напряжения на стенке [4,5,9] 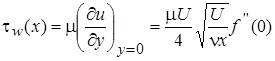 . (2.12)
. (2.12)
В этом уравнении 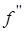 (0)=1,328. Тогда безразмерное касательное напряжение на стенке
(0)=1,328. Тогда безразмерное касательное напряжение на стенке
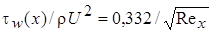 . (2.13)
. (2.13)
Из (2.13) видно, что сопротивление трения Cf, выраженное через 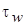 , уменьшается по длине пластины, т.е.
, уменьшается по длине пластины, т.е. 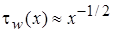 . Такая пропорциональность между касательным напряжением и продольной координатой обусловлена образованием и закономерностью развития пограничного слоя на стенке.
. Такая пропорциональность между касательным напряжением и продольной координатой обусловлена образованием и закономерностью развития пограничного слоя на стенке.
Для практики очень важно знать местный и средний коэффициенты сопротивления [4]
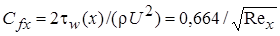 , (2.14)
, (2.14)
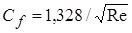 . (2.15)
. (2.15)
Аналогично образованию гидродинамического пограничного слоя, обтекаемого реальной жидкостью, над поверхностью, имеющей температуру, отличающуюся от температуры потока, образуется тепловой пограничный слой. Изменение температуры пристенного потока происходит на весьма небольшом расстоянии от стенки. Эта пристенная область, в которой в направлении, перпендикулярном поверхности, существует градиент температуры, называется температурным, или тепловым, пограничным слоем, который в наиболее общем виде может быть обобщен уравнением энергии (1.3). Соотношение между тепловым и гидродинамическим слоями, в основном, зависит от рода жидкости. Учитывая изменение физических свойств с температурой, температурный пограничный слой можно представить уравнением энергии в следующем виде:
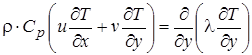 . (2.16)
. (2.16)
Уравнения законов теплоотдачи и теплопроводности, а также уравнение теплообмена: 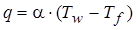 , (2.17)
, (2.17)
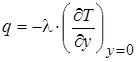 , (2.18)
, (2.18)
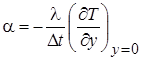 . (2.19)
. (2.19)
В случае постоянных, т.е. не зависящих от температуры физических свойств, уравнение энергии (2.16) запишется в виде:
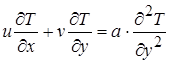 . (2.20)
. (2.20)
Введем вместо координаты T другую, безразмерную координату
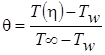 . (2.21)
. (2.21)
После ввода безразмерных параметров, по аналогии представленной выше для уравнения (2.4), уравнение (2.20) можно преобразовать в обыкновенное дифференциальное уравнение, выражающее температурное поле в пограничном слое: 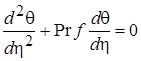 . (2.22)
. (2.22)
Поле скоростей не зависит от температурного поля, поэтому сначала нужно решить гидродинамические уравнения и полученные результаты можно использовать для определения температурного поля.
Число Прандтля характеризует теплофизические свойства теплоносителей. В физическом смысле Pr является как бы мерой подобия полей температуры и скорости. При Pr=1, поля температуры и скорости подобны. Следовательно, при вынужденном конвективном течении число Прандтля отражает отношение толщин температурного и динамического пограничных слоев: 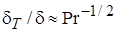 .
.
В жидкостях числа Прандтля больше единицы, поэтому динамический пограничный слой толще температурного, а в различных маслах числа Прандтля достигают нескольких десятков тысяч, поэтому температурный пограничный слой расположен в вязком подслое.
В литературе [1,4], после численного решения уравнения (2.22) предлагаются зависимости для чисел Нуссельта
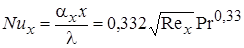 , (2.23)
, (2.23)
а для определения средней теплоотдачи
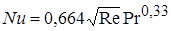 . (2.24)
. (2.24)
Дата добавления: 2020-10-25; просмотров: 1043;











