Интерференция в тонких пленках
Рассмотрим теперь случай с тонкой пластиной, с плоскими и необязательно параллельными поверхностями (рис. 8.21).
| |
Пусть пластину освещает точечный источник S, и мы рассматриваем результат интерференции в произвольной точке Р. Интерференционная картина в общем случае не локализована. Оптическая разность хода интерферирующих волн равна:
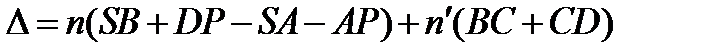 . (8.21)
. (8.21)
Вычислить ∆ для произвольного случая весьма сложно, однако, если пластинка тонкая, то можно считать, что точки B, A, D почти совпадают, тогда
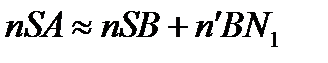 ;
; 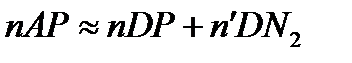 ,
,
где AN1 и AN2 — перпендикуляры к BC и CD.
Подставляя в (8.21), получаем
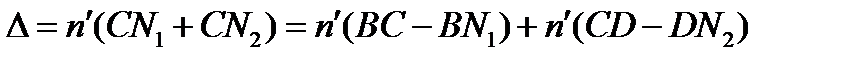 .
.
Если угол между поверхностями пленки мал, то
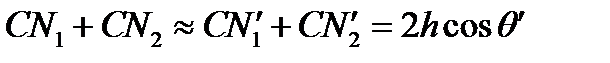 .
.
Следовательно, получим, как и раньше
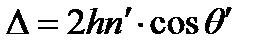 ;
; 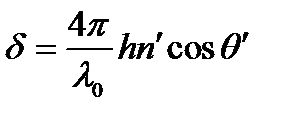 .
.
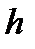 и
и 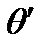 зависят от положения источника S, и, даже при незначительном увеличении размеров источника, область значений δ в Р от разных точек источника становится такой большой, что полосы исчезают. Тем не менее, существует специальный частный случай, когда вид интерференционных полос незначительно зависит от размеров источника. Этот случай характеризуется тем, что точка Р находится в пленке. При этом, для того, чтобы рассмотреть картину, необходимо либо сфокусировать глаз на пленку, либо перенести её с пленки на экран с помощью какой-либо оптической системы. В этом случае
зависят от положения источника S, и, даже при незначительном увеличении размеров источника, область значений δ в Р от разных точек источника становится такой большой, что полосы исчезают. Тем не менее, существует специальный частный случай, когда вид интерференционных полос незначительно зависит от размеров источника. Этот случай характеризуется тем, что точка Р находится в пленке. При этом, для того, чтобы рассмотреть картину, необходимо либо сфокусировать глаз на пленку, либо перенести её с пленки на экран с помощью какой-либо оптической системы. В этом случае 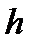 практически одинаково для всех пар лучей, приходящих в точку P', сопряженную с Р от различных точек протяженного источника (см. рис. 8.22), и тогда разброс величины δ в точке P' вызывается главным образом различием
практически одинаково для всех пар лучей, приходящих в точку P', сопряженную с Р от различных точек протяженного источника (см. рис. 8.22), и тогда разброс величины δ в точке P' вызывается главным образом различием 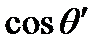 . Если диапазон изменения
. Если диапазон изменения 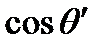 достаточно мал, то этот диапазон в точке P' много меньше 2π даже с источником значительных размеров, и полосы отчетливо видны. Очевидно, что в этом случае они локализованы в пленке. Практически условие малости интервала изменения
достаточно мал, то этот диапазон в точке P' много меньше 2π даже с источником значительных размеров, и полосы отчетливо видны. Очевидно, что в этом случае они локализованы в пленке. Практически условие малости интервала изменения 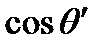 можно выполнить при наблюдении по нормали к пленке или при ограничении входного зрачка, хотя зрачок невооруженного глаза и сам по себе может быть достаточно мал.
можно выполнить при наблюдении по нормали к пленке или при ограничении входного зрачка, хотя зрачок невооруженного глаза и сам по себе может быть достаточно мал.
| |
Учитывая изменение фазы на π радиан при отражении от одной из поверхностей пленки, получаем выражение для оптической разности хода
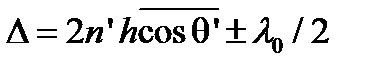 , (8.22)
, (8.22)
где 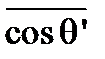 - среднее значение
- среднее значение 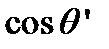 для точек источника, от которых свет доходит до P'. Условие
для точек источника, от которых свет доходит до P'. Условие 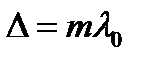 при
при 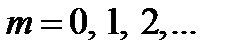 соответствует максимуму интенсивности, а при
соответствует максимуму интенсивности, а при 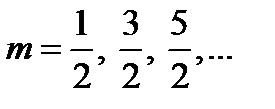 - минимуму интенсивности.
- минимуму интенсивности.
Величина 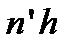 — есть оптическая толщина в Р, и, следовательно, интерференция в Р не зависит от толщины пленки в других местах. Отсюда следует, что соотношения (8.22) остаются справедливыми даже для неплоских поверхностей пленки при условии, что угол между ними остается малым. Тогда, если
— есть оптическая толщина в Р, и, следовательно, интерференция в Р не зависит от толщины пленки в других местах. Отсюда следует, что соотношения (8.22) остаются справедливыми даже для неплоских поверхностей пленки при условии, что угол между ними остается малым. Тогда, если 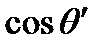 при регистрации картины изменяется незначительно, то интерференционные полосы соответствуют совокупности мест пленки, где оптические толщины одинаковы. По этой причине такие полосы часто называют полосами равной толщины. На этом основано, например, определение качества оптических деталей с помощью колец Ньютона (рис. 8.23).
при регистрации картины изменяется незначительно, то интерференционные полосы соответствуют совокупности мест пленки, где оптические толщины одинаковы. По этой причине такие полосы часто называют полосами равной толщины. На этом основано, например, определение качества оптических деталей с помощью колец Ньютона (рис. 8.23).
| |
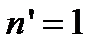 ), в которой возникает интерференционная картина. Условие минимумов в ней имеет вид:
), в которой возникает интерференционная картина. Условие минимумов в ней имеет вид:
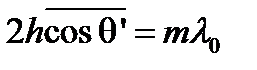
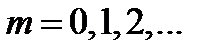 (8.23)
(8.23)
На практике обычно 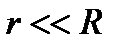 , тогда при наблюдении по нормали (
, тогда при наблюдении по нормали ( 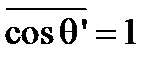 )
)
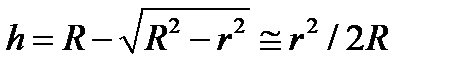 ,
,
и тогда получаем:
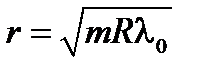 ,
,
то есть радиусы темных колец пропорциональны корню квадратному из целых чисел.
Изложенный метод колец Ньютона широко используется в производстве для контроля качества изготовления линз. В этом случае линза с контролируемым радиусом 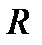 накладывается на сферическую поверхность с известным эталонным радиусом
накладывается на сферическую поверхность с известным эталонным радиусом 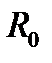 . Воздушный промежуток
. Воздушный промежуток 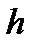 на радиусе
на радиусе 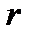 при этом будет равен
при этом будет равен
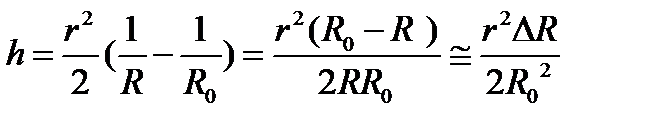 . (8.24)
. (8.24)
Из (8.23) с учетом (8.24) находим: 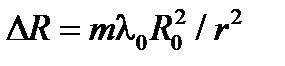 , т.е. погрешность
, т.е. погрешность 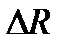 изготовления радиуса линзы зависит от числа
изготовления радиуса линзы зависит от числа 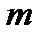 наблюдаемых интерференционных колец. По искривлению интерференционных колец судят о местных ошибках контролируемой поверхности. Обычно допустимые местные ошибки задаются в долях
наблюдаемых интерференционных колец. По искривлению интерференционных колец судят о местных ошибках контролируемой поверхности. Обычно допустимые местные ошибки задаются в долях 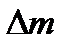 ширины интерференционной полосы.
ширины интерференционной полосы.
Если пленка представляет собой клин с малым углом α при вершине, то 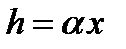 , где
, где 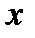 — расстояние от точки Р до вершины клина, тогда условие минимумов будет совпадать с (8.23) и расстояние
— расстояние от точки Р до вершины клина, тогда условие минимумов будет совпадать с (8.23) и расстояние 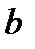 между соседними полосами найдется из выражения
между соседними полосами найдется из выражения
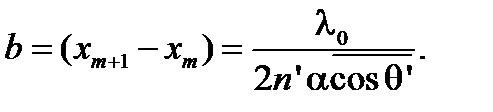
При наблюдении по нормали к поверхности клина 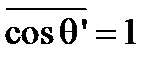 и тогда
и тогда
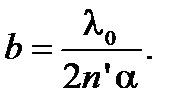
Дата добавления: 2020-03-21; просмотров: 740;











