Источники в виде щели, видность полос
Все сказанное выше относилось к точечному источнику. Однако все реальные источники имеют конечные размеры и поэтому необходимо выяснить влияние их размеров на интерференционную картину. Будем считать, что реальные источники состоят из точечных взаимно некогерентных источников. Тогда, естественно, интенсивность в любой точке поля равна сумме интенсивностей от каждого точечного источника.
Во всех описанных устройствах интерференционные полосы перпендикулярны плоскости, в которой находятся первичный источник S и вторичные источники S1 и S2 и, следовательно, если S смещать перпендикулярно этой плоскости, то полосы будут просто смещаться вдоль своих направлений. Таким образом, использование линейного источника (или на практике достаточно узкой щели), расположенного в этом направлении, не приведет к ухудшению четкости полос. Аналогично в опыте Юнга отверстия можно заменить узкими щелями параллельными щели источника. Таким путем можно значительно увеличить интенсивность интерференционной картины.
Для получения более яркой картины следует также увеличивать и ширину щели источника, однако это может привести к тому, что полосы станут менее четкими. Рассмотрим это подробнее.
| |
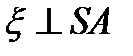 в
в 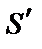 . Следовательно,
. Следовательно, | d |
| S2 |
| с |
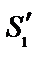 и
и 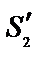 и с
и с 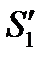
|
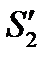
|
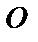 в точку
в точку 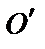 , т. к. она расположена на перпендикуляре к середине отрезка
, т. к. она расположена на перпендикуляре к середине отрезка 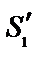
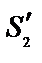 (Δ=0). Если отрезок
(Δ=0). Если отрезок 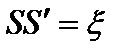 , то
, то 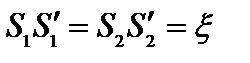 , и
, и
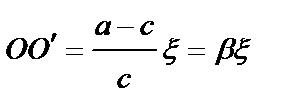 , где
, где 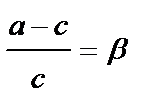 .
.
Найдем оптические разности хода  и
и 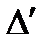 соответственно от источников
соответственно от источников 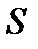 и
и 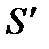 в произвольной точке Р поля.
в произвольной точке Р поля.
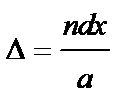 ;
; 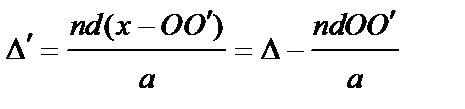 . (8.10)
. (8.10)
Подставляя в (8.10) значение 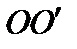 ,получаем:
,получаем:
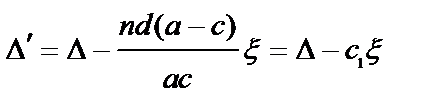 ,
,
где с1 – безразмерный коэффициент, равный
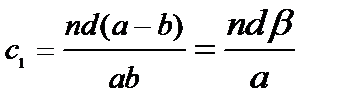 . (8.11)
. (8.11)
Соответствующая разность фаз равна
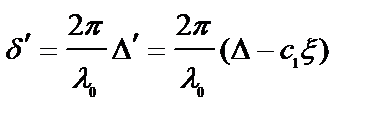 (8.12)
(8.12)
Пусть теперь источником является щель шириной  . Разобьем ее на элементарные полоски шириной
. Разобьем ее на элементарные полоски шириной 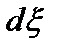 и будем считать полоску равнояркой. Тогда интенсивность света в произвольной точке Р от одной полоски, расположенной на расстоянии
и будем считать полоску равнояркой. Тогда интенсивность света в произвольной точке Р от одной полоски, расположенной на расстоянии 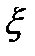 от оси будет равна, очевидно (см. формулу (8.4)):
от оси будет равна, очевидно (см. формулу (8.4)):
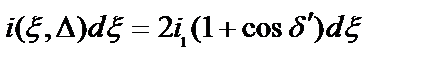 ,
,
где 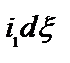 - интенсивность в точке Р от полоски лишь от одного зеркала.
- интенсивность в точке Р от полоски лишь от одного зеркала.
Поскольку излучение элементарных полосок некогерентно, то полная интенсивность с учетом (8.12) будет равна:
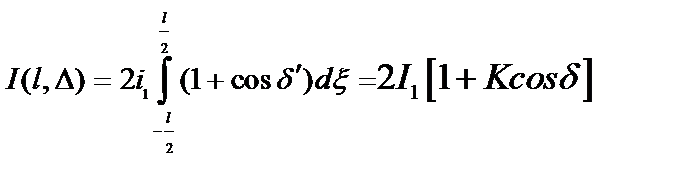 , (8.13)
, (8.13)
где 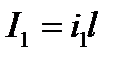 - интенсивность в точке Р от источника, образованная одним зеркалом,
- интенсивность в точке Р от источника, образованная одним зеркалом, 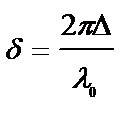 - разность фаз в точке Р от центра источника.
- разность фаз в точке Р от центра источника.
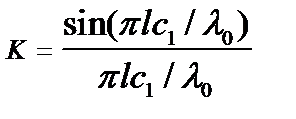 .
.
Полученное выражение (8.13) отличается от идеального случая (8.4)
коэффициентом К, стоящим перед 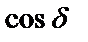 .
.
График зависимости интенсивности от 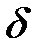 представлен на рис. 8.11.
представлен на рис. 8.11.
| |
Легко показать, что коэффициент К определяет контраст возникающей интерференционной картины. Действительно, контраст (видность) обычно определяют следующим образом:
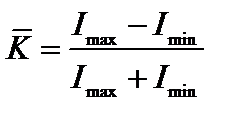 .
.
Поскольку из (8.13)
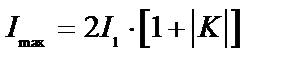 ;
; 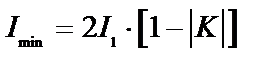 ,
,
то
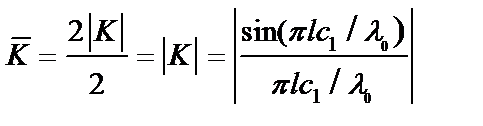 ;
;
На рисунке 8.12 представлен график зависимости контраста 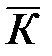 от ширины источника
от ширины источника  .
.
| |
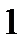
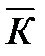
 . Найдем допустимый размер
. Найдем допустимый размер 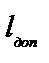 источника, при котором видность интерференционной картины еще остается высокой. Обычно считают значение
источника, при котором видность интерференционной картины еще остается высокой. Обычно считают значение 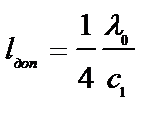 , т.к при этом
, т.к при этом 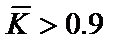 , т.е. контраст картины снижается незначительно.
, т.е. контраст картины снижается незначительно.
Подставляя значение 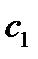 из (8.11) в
из (8.11) в 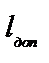 получаем:
получаем:
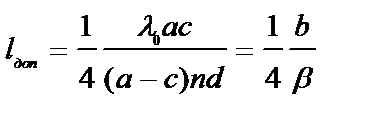 , (8.14)
, (8.14)
где 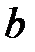 – ширина интерференционной полосы.
– ширина интерференционной полосы.
Из (8.14) видно, что 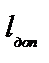 зависит от расстояния
зависит от расстояния 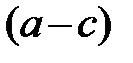 от зеркал до плоскости наблюдения.
от зеркал до плоскости наблюдения.
8.1.6 Интерферометр Релея. Измерение оптической разности хода 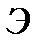
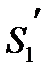
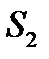
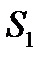
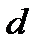
| |
Возвращаясь к опыту Юнга можно заметить, что с энергетической точки зрения этот прибор не совсем удачен для получения интенсивной картины, поскольку максимум интенсивности от каждого источника находится в разных точках А и В (рис.8.13).Однако, если с помощью линзы Л свести лучи 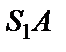 и
и 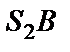 в точку О (показано пунктиром), то в этой точке можно получить картину высокой интенсивности. Кстати, при этом расстояние d между источниками можно значительно увеличить без заметных энергетических потерь. Естественно, что расстояние между соседними полосами по-прежнему будет равно
в точку О (показано пунктиром), то в этой точке можно получить картину высокой интенсивности. Кстати, при этом расстояние d между источниками можно значительно увеличить без заметных энергетических потерь. Естественно, что расстояние между соседними полосами по-прежнему будет равно 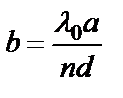 , и если линза идеальная (т.е не вносит разности хода в интерферирующие пучки), то полоса нулевого порядка также совпадет с точкой О. Если же вносится разность хода Δ, то смещение полосы в т. О составит величину:
, и если линза идеальная (т.е не вносит разности хода в интерферирующие пучки), то полоса нулевого порядка также совпадет с точкой О. Если же вносится разность хода Δ, то смещение полосы в т. О составит величину:
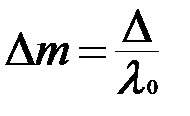 ,
,
измеряемую в долях ширины полосы 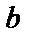 . Это, кстати говоря, используется при проверке качества линз. Если измерять
. Это, кстати говоря, используется при проверке качества линз. Если измерять 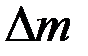 при одном неподвижном источнике
при одном неподвижном источнике 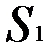 , а другом изменяющимся, например от
, а другом изменяющимся, например от 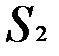 до
до 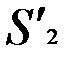 , то можно определить разность хода
, то можно определить разность хода  и, следовательно, разность фаз
и, следовательно, разность фаз 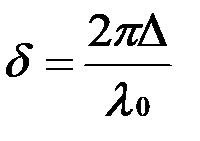 по всей апертуре линзы. Такой интерферометр получил название интерферометра Релея, правда на практике он часто используется в несколько измененном виде (рис. 8.14). Источник света
по всей апертуре линзы. Такой интерферометр получил название интерферометра Релея, правда на практике он часто используется в несколько измененном виде (рис. 8.14). Источник света 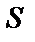 здесь находится в переднем фокусе линзы и отверстия
здесь находится в переднем фокусе линзы и отверстия 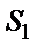 и
и 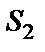 освещаются параллельным пучком лучей. Линза
освещаются параллельным пучком лучей. Линза 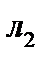 сводит интерферирующие пучки в т. О.
сводит интерферирующие пучки в т. О.
| |
Эта схема удобна тем, что в промежутках между 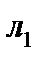 и
и 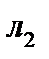 можно устанавливать различные объекты для измерения оптической разности хода. Лучше всего неискажающие геометрию лучей, то есть в виде плоских пластинок. Чаще всего такой интерферометр служит для измерения показателей преломления газов. Обычно для этого устанавливают две идентичные кюветы длиной
можно устанавливать различные объекты для измерения оптической разности хода. Лучше всего неискажающие геометрию лучей, то есть в виде плоских пластинок. Чаще всего такой интерферометр служит для измерения показателей преломления газов. Обычно для этого устанавливают две идентичные кюветы длиной  и, если показатели преломления газов в кюветах
и, если показатели преломления газов в кюветах 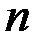 и
и 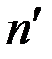 , то возникающая разность хода
, то возникающая разность хода 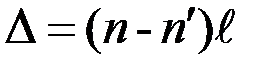 , и, следовательно, порядок интерференции в точке О изменится на величину
, и, следовательно, порядок интерференции в точке О изменится на величину
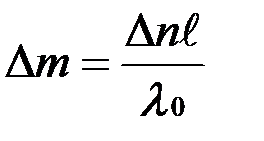
Измерение ведется в белом свете, поэтому 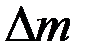 легко регистрируется по смещению ахроматической полосы. При
легко регистрируется по смещению ахроматической полосы. При 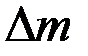 =0,1;
=0,1; 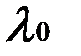 = 0,5 мкм;
= 0,5 мкм;  =1 м получаем:
=1 м получаем:
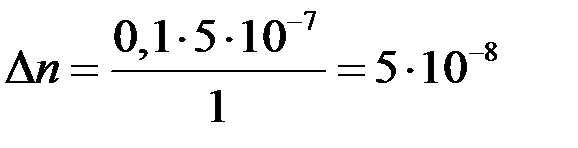 - очень высокая точность!
- очень высокая точность!
Стоячие волны
В рассмотренных устройствах две интерферирующие волны распространяются вблизи точки наблюдения почти в одном направлении. Теперь мы рассмотрим интерференцию двух волн, распространяющихся в противоположных направлениях, например, интерференцию падающей и отраженной плоских монохроматических волн света при его падении на хорошо отражающую плоскую поверхность. Предположим, что такой поверхностью является плоскость 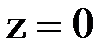 с положительной осью z, направленной в сторону среды, в которой идёт падающая волна (рис. 8.15):
с положительной осью z, направленной в сторону среды, в которой идёт падающая волна (рис. 8.15):
| |
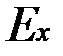 , равную
, равную
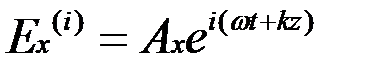 ,
,
где по-прежнему 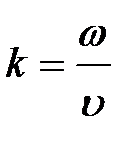 , а знак «+» перед
, а знак «+» перед 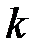 показывает, что волна распространяется в направлении (
показывает, что волна распространяется в направлении ( 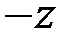 ). Будем считать вторую поверхность металлической средой, тогда с учетом скачкообразного изменения фазы волны на
). Будем считать вторую поверхность металлической средой, тогда с учетом скачкообразного изменения фазы волны на 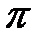 радиан для отраженной волны можно записать:
радиан для отраженной волны можно записать: 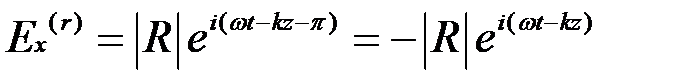 ,
,
где 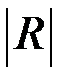 - модуль комплексной амплитуды колебаний отраженной волны. Для простоты положим, что амплитудный коэффициент отражения от поверхности равен единице, т.е
- модуль комплексной амплитуды колебаний отраженной волны. Для простоты положим, что амплитудный коэффициент отражения от поверхности равен единице, т.е 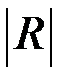 =
= 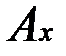 , тогда поле в первой среде будет равно
, тогда поле в первой среде будет равно 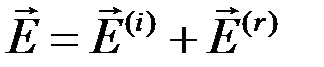 и, следовательно
и, следовательно
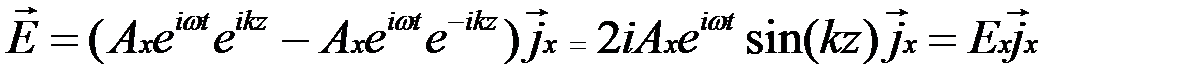 , (8.15)
, (8.15)
где 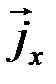 - единичный вектор, коллинеарный оси
- единичный вектор, коллинеарный оси 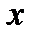 ,
, 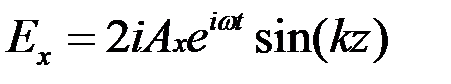 .
.
Найдем вектор 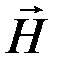 падающей и отраженной волн.
падающей и отраженной волн.
Вектор 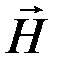 в бегущей волне связан с
в бегущей волне связан с 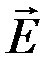 соотношением
соотношением
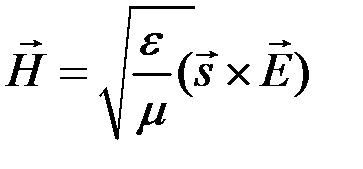 , (8.16)
, (8.16)
где 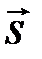 - единичный вектор направления распространения волны, т.е.
- единичный вектор направления распространения волны, т.е. 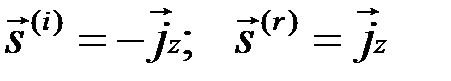 .
.
Примем магнитную проницаемость среды 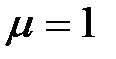 , тогда из (8.16) получаем:
, тогда из (8.16) получаем:
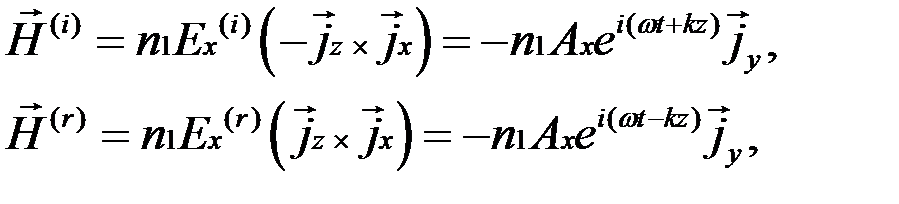
где 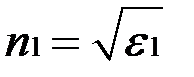 .
.
Следовательно
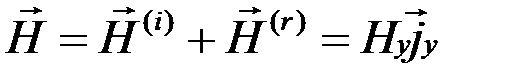 ,
,
где
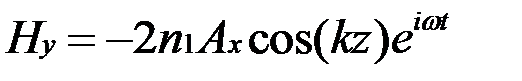 .
.
Выражение (8.15) показывает, что в первой среде уже не существует распространяющихся волн. (отсутствует член ( 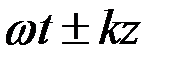 )). В каждой точке среды вектор
)). В каждой точке среды вектор 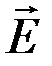 осциллирует в плоскости xoz, c частотой
осциллирует в плоскости xoz, c частотой  и амплитудой
и амплитудой 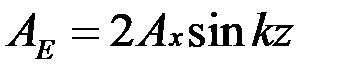 ,зависящей от
,зависящей от 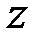 . В частности, имеются точки, где амплитуда колебаний равна нулю. Эти точки называются узлами вектора
. В частности, имеются точки, где амплитуда колебаний равна нулю. Эти точки называются узлами вектора 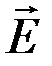 стоячей волны.
стоячей волны.
Они определяются выражением: 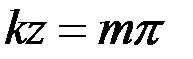 , где
, где 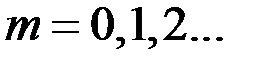 , откуда
, откуда 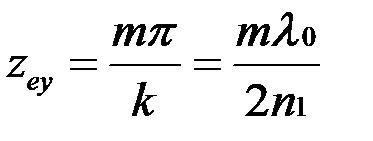 , при
, при 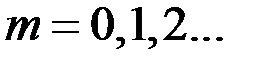 .
.
Точки с максимальной амплитудой колебаний электрического вектора называются пучностями. Пучности имеют место в точках:
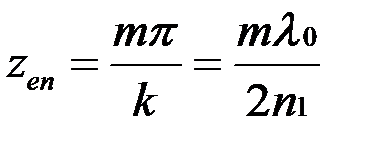 , при
, при 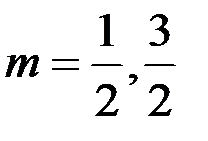 ….
….
вектор 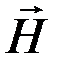 магнитного поля осциллирует в плоскости yoz, c той же частотой и амплитудой
магнитного поля осциллирует в плоскости yoz, c той же частотой и амплитудой 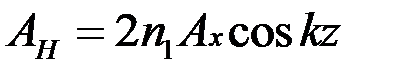 , поэтому положения узлов вектора
, поэтому положения узлов вектора 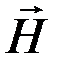 определяется выражением:
определяется выражением: 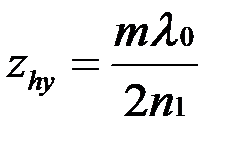 , при
, при 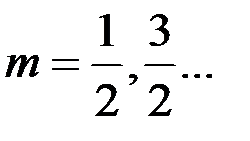 , а пучностей –
, а пучностей – 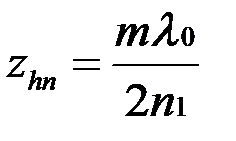 при
при 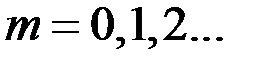 . . Таким образом, в стоячей волне узлы магнитного поля совпадают с пучностями электрического и наоборот.
. . Таким образом, в стоячей волне узлы магнитного поля совпадают с пучностями электрического и наоборот.
Существование стоячих световых волн впервые было экспериментально установлено Винером. В основе метода Винера лежали теоретические положения о том, что химические процессы в фотоэмульсиях при воздействии света происходят только за счет электрического вектора 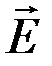 электромагнитного поля. Алюминированное зеркало 3 освещалось параллельным пучком квазимонохроматического света (рис. 8.16). На зеркало под небольшим углом устанавливалась фотопластинка с тонким слоем фотоэмульсии. После проявления были обнаружены черные эквидистантные полосы и прозрачные области между ними. Места почернения располагались как раз в области пучностей электрического поля.
электромагнитного поля. Алюминированное зеркало 3 освещалось параллельным пучком квазимонохроматического света (рис. 8.16). На зеркало под небольшим углом устанавливалась фотопластинка с тонким слоем фотоэмульсии. После проявления были обнаружены черные эквидистантные полосы и прозрачные области между ними. Места почернения располагались как раз в области пучностей электрического поля.
| |
Чтобы выяснить распространение электромагнитной энергии в стоячей волне, найдём вектор Пойнтинга. Поскольку по определению вектор Пойнтинга 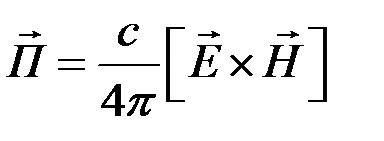 , то есть является нелинейным преобразованием над векторами электромагнитного поля, то математически более корректно определять его следующим образом:
, то есть является нелинейным преобразованием над векторами электромагнитного поля, то математически более корректно определять его следующим образом:
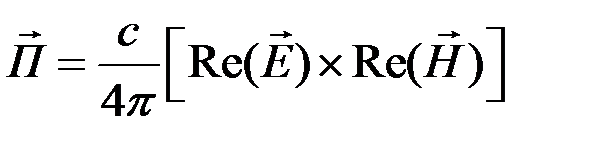 ,
,
где
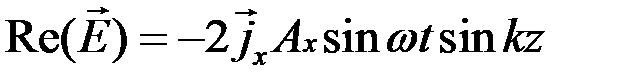
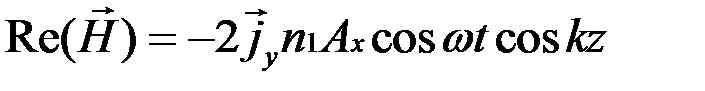
С учетом этого получаем:
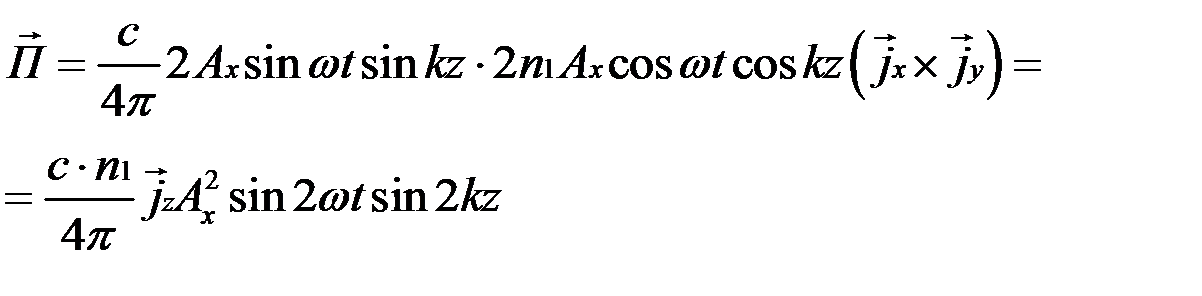
Построим графическое изображение векторов 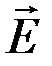 и
и 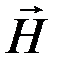 поля и вектора Пойнтинга в стоячей волне. Прежде всего отметим, что в моменты времени
поля и вектора Пойнтинга в стоячей волне. Прежде всего отметим, что в моменты времени 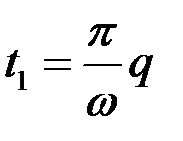 , где
, где 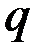 - целое число, вектора
- целое число, вектора 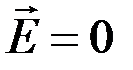 и
и 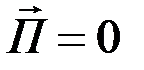 ; а в моменты времени
; а в моменты времени 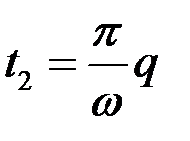 , где
, где 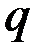 - полуцелое число,
- полуцелое число, 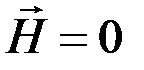 и
и 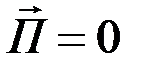 . В промежутках между этими моментами все три вектора отличны от нуля. Графическое представление векторов
. В промежутках между этими моментами все три вектора отличны от нуля. Графическое представление векторов 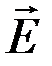 и
и 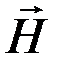 поля стоячей волны, а также компоненты
поля стоячей волны, а также компоненты 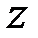 вектора Пойнтинга в момент времени
вектора Пойнтинга в момент времени 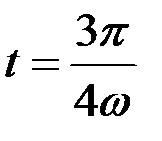 показано на рисунке 8.17.
показано на рисунке 8.17.
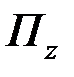 обозначены направления распространения электромагнитной энергии.
обозначены направления распространения электромагнитной энергии.
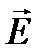 , , 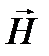 и вектор Пойнтинга в стоячей волне и вектор Пойнтинга в стоячей волне
|
Поскольку поток энергии отсутствует в точках, где, либо 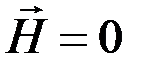 , либо
, либо 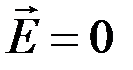 , то, следовательно, через узлы электрического и магнитного полей энергия не перетекает. Поток энергии имеет место лишь в промежутках между узлами из-за превращения энергии электрического поля в магнитную и наоборот.
, то, следовательно, через узлы электрического и магнитного полей энергия не перетекает. Поток энергии имеет место лишь в промежутках между узлами из-за превращения энергии электрического поля в магнитную и наоборот.
Деление амплитуды
Дата добавления: 2020-03-21; просмотров: 831;











