Интерференционные полосы в квазимонохроматическом и белом свете
До сих пор мы предполагали, что первичный точечный источник испускает монохроматическое излучение. Теперь мы это ограничение снимем и предположим, что зеркала Френеля освещены полихроматическим светом от точечного источника S. Такой свет можно представить, как сумму некогерентных монохроматических компонент, занимающих некоторый частотный диапазон Δν или диапазон длин волн Δλ. Поскольку эти компоненты взаимно некогерентны, то при наложении их в некоторой плоскости анализа полная интенсивность в любой точке плоскости равна сумме интенсивностей интерференционных картин, образуемых каждой монохроматической компонентой. Пусть диапазон длин волн источника равен Δλ , а средняя длина волны 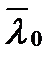 (рис. 8.8).
(рис. 8.8).
| |
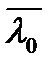
|
| Δλ |
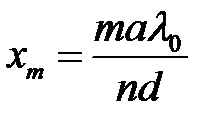 ,
,
а значение λ0 всех компонент заключено в диапазоне Δλ , то максимумы "m"-го порядка займут в плоскости наблюдения отрезок (рис. 8.9):
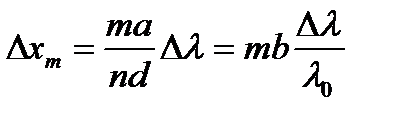 , (8.6)
, (8.6)
| |
Отсюда видно, что «размазывание» 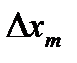 m - го максимума увеличивается с ростом порядка интерференции m.
m - го максимума увеличивается с ростом порядка интерференции m.
Рассмотрим сначала случай, когда диапазон длин волн Δλ мал по сравнению со средней длиной волны λ0, т.е когда
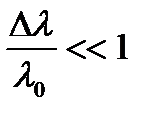 или
или 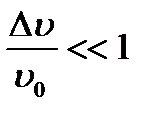 . (8.7)
. (8.7)
Свет, удовлетворяющий условию (8.7), называют квазимонохроматическим. Если для поля наблюдений
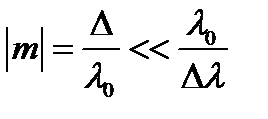 (8.8)
(8.8)
или, что тоже самое
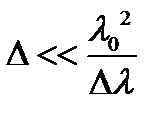 , (8.9)
, (8.9)
то отрезок 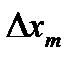 , как следует из (8.6), будет значительно меньше ширины одной полосы, т.е.
, как следует из (8.6), будет значительно меньше ширины одной полосы, т.е.
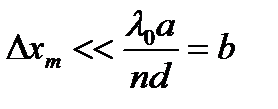
В этом случае величиной 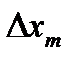 можно пренебречь по сравнению с
можно пренебречь по сравнению с 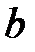 и “размазывание” интерференционной картины будет мало заметно, т.е. интерференционные полосы будут такими же четкими, как и для строго монохроматического света с длиной волны λ0.
и “размазывание” интерференционной картины будет мало заметно, т.е. интерференционные полосы будут такими же четкими, как и для строго монохроматического света с длиной волны λ0.
Если свет квазимонохроматический, но условие (8.8) не выполняется, то полосы будут менее отчетливыми, чем в монохроматическом свете и полная интенсивность будет зависеть от распределения интенсивностей среди монохроматических компонент. Для оценки можно считать, что интерференционная картина становится неразличимой, когда
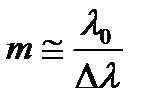 или
или 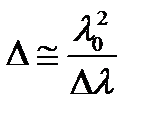 .
.
В этом случае максимумы “m”-го порядка занимают отрезок 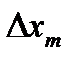 , равный ширине полосы b. Если свет не квазимонохроматичен, т.е. условие (8.7) не выполняется, то наблюдаемая картина зависит также от спектральной чувствительности приемника излучения. В практически важном случае белого света и визуального наблюдения отношение
, равный ширине полосы b. Если свет не квазимонохроматичен, т.е. условие (8.7) не выполняется, то наблюдаемая картина зависит также от спектральной чувствительности приемника излучения. В практически важном случае белого света и визуального наблюдения отношение 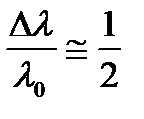 . В этом случае в том месте, где для монохроматического света любой длины волны располагается полоса нулевого порядка, мы увидим центральную белую полосу. По обе стороны от этой полосы будут видны окрашенные максимумы и минимумы, а за ними пространство, которое кажется глазу равномерно освещенным белым светом. Однако это не обычный белый свет. Так на расстоянии
. В этом случае в том месте, где для монохроматического света любой длины волны располагается полоса нулевого порядка, мы увидим центральную белую полосу. По обе стороны от этой полосы будут видны окрашенные максимумы и минимумы, а за ними пространство, которое кажется глазу равномерно освещенным белым светом. Однако это не обычный белый свет. Так на расстоянии 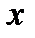 от центральной белой полосы располагаются максимумы интенсивностей для длин волн
от центральной белой полосы располагаются максимумы интенсивностей для длин волн
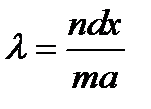 , где
, где 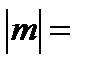 1, 2, 3…
1, 2, 3…
и минимумы для длин волн
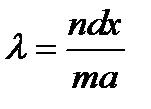 , где
, где 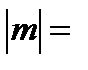 1/2, 3/2, 5/2… .
1/2, 3/2, 5/2… .
Следовательно, если в этом месте расположить входную щель спектрометра параллельно полосам в монохроматическом свете, то спектр будет пересекаться светлыми и темными полосами. Это один из примеров так называемого канавчатого спектра.
Дата добавления: 2020-03-21; просмотров: 717;











