Деление волнового фронта

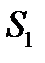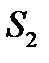Первую экспериментальную установку для демонстрации явления интерференции осуществил Т. Юнг (1801 г.). Свет от точечного монохроматического источника S падал на два небольших отверстия и в экране A (рис. 8.2), расположенных рядом и находящихся на равных расстояниях от оси z. Эти источники действуют как вторичные монохроматические точечные и синфазные источники, а световые пучки от них перекрываются позади экрана. Интерференция наблюдается в области перекрытия световых пучков.

Рис. 8.2 Схема эксперимента Юнга

Рассмотрим интерференционную картину в плоскости P, находящейся на расстоянии 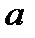от экрана A, нормальной перпендикуляру CO, восстановленному в середине отрезка 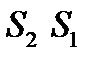. Введем в плоскости P систему координат xyz, так, что ее ось x направлена параллельно линии 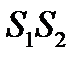, а ось z совпадает с CO (рис. 8.3). Тогда для расстояни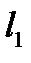й и 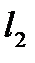от источников 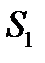и 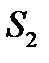до произвольной точки P 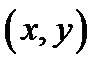в плоскости P получаем:

Рис. 8.3. Схема для расчёта параметров интерференционной картины

; ,

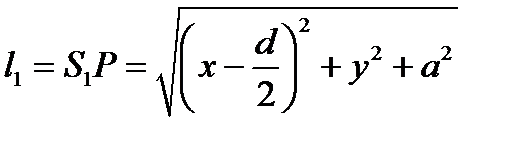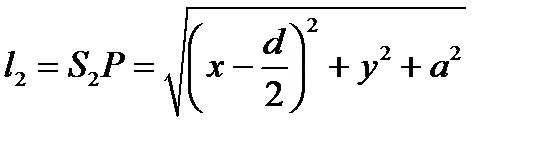и, следовательно, 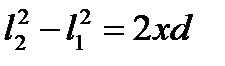, т.е. .

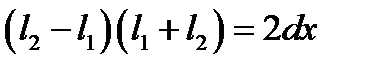Геометрическая разность хода

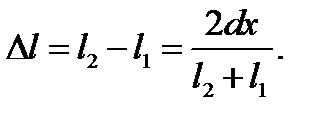
Вследствие малости оптических длин волн интерференционная картина будет наблюдаться, если 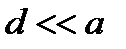. При этом условии справедливо приближение:

,

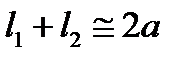поэтому 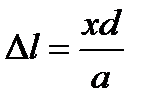и соответствующая оптическая разность хода

,

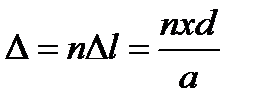а разность фаз

.

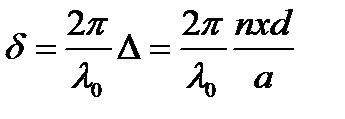Здесь 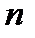-показатель преломления среды.

Так как угол 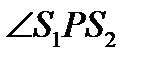очень мал, то можно считать, что волны движутся к точке P по одному направлению, т.е. можно распространить полученные ранее результаты, а именно, интенсивность в интерференционной картине рассчитывать по формуле (8.3). Интенсивность будет постоянной в точках, где 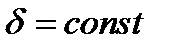, в частности в точках с координатами

,

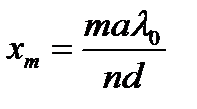при 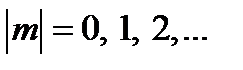она будет максимальной, а при 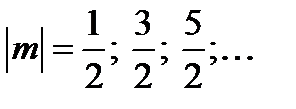− минимальной. Расстояние между соседними максимумами (ширина интерференционных полос) равно

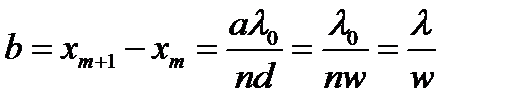, (8.5)
где 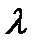– длина волны в среде, 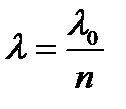, 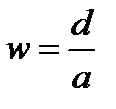– угол сходимости интерферирующих пучков.

Таким образом, интерференционная картина представляет собой равноотстоящие друг от друга полосы, параллельные оси 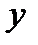, т.е. перпендикулярные отрезку 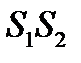. Число 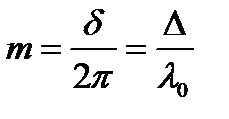называется порядком интерференции: светлым полосам соответствуют целые порядки интерференции, а темным – полуцелые.