Интерференция двух монохроматических волн

Рассмотрим плоскую волну, для которой объемная плотность электромагнитной энергии определяется как

,

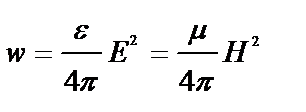скорость распространения:

,

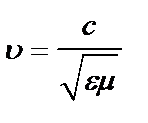вектор Пойнтинга:

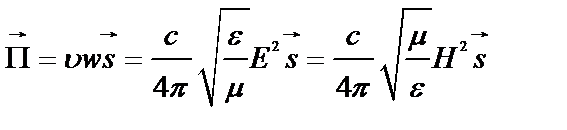, (8.1)
где 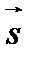− единичный вектор в направлении распространения волны, 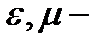диэлектрическая и магнитная проницаемости среды соответственно.

Определим для этой волны интенсивность как среднее по времени значение модуля вектора Пойнтинга, т.е. 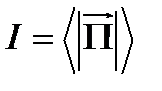, где усреднение производится за время, значительно большее, чем период колебаний. Целесообразность введения такого понятия об интенсивности объясняется следующими соображениями:

− как видно из (8.1), мгновенная интенсивность 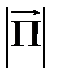колеблется с большой частотой 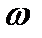(в оптике 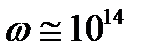1/с.), и это изменение не может быть зарегистрировано ни одним детектором;

− введенное значение интенсивности имеет ясный физический смысл – это усредненное значение количества электромагнитной энергии, которое проходит через единичную площадку, перпендикулярную распространению потока энергии в единицу времени.

Таким образом:

,

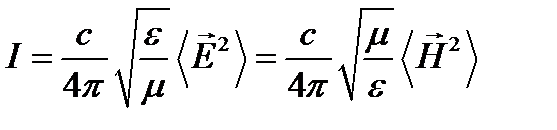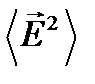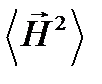В дальнейшем коэффициенты перед или мы будем опускать и считать для простоты, что 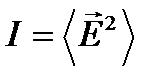или .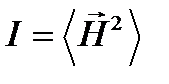

Воспользовавшись комплексным представлением для описания электромагнитной волны запишем вектор 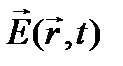в виде

,

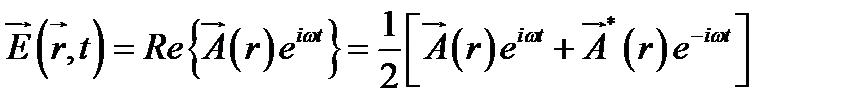где 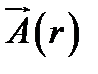− комплексная амплитуда – вектор с декартовыми координатами:

.

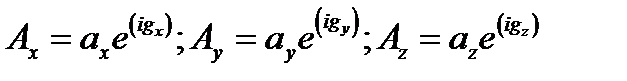Здесь 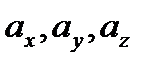– действительные компоненты амплитуды колебаний,

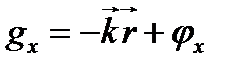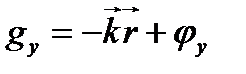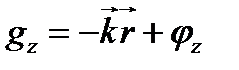; ; – фазы колебаний, 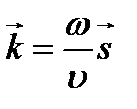- волновой вектор, 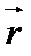- радиус вектор точки, 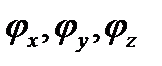- начальные фазы, определяющие состояние поляризации волны (например, для плоской волны, идущей вдоль оси z, 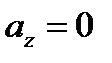, при 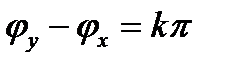– линейная поляризация, при 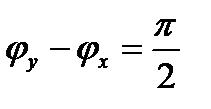– эллиптическая поляризация и т.п.).

Найдем квадрат модуля электрического вектора :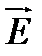

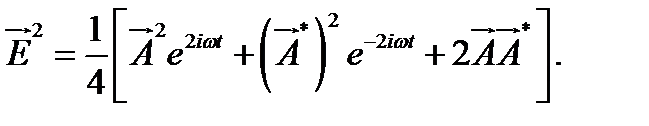
Интенсивность волны:

,
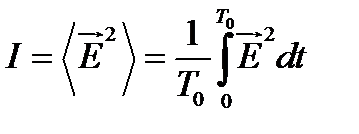где 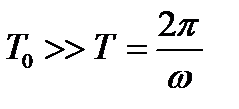. Здесь 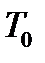– время усреднения, 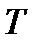– период колебаний.

Поскольку 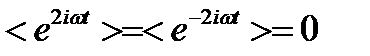, то

,
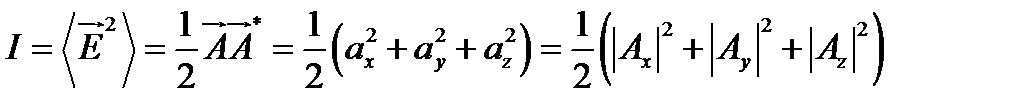следовательно, интенсивность равна половине квадрата модуля комплексной амплитуды.

Пусть теперь в некоторой точке P происходит суперпозиция двух плоских волн с одинаковыми частотами 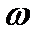. Результирующее поле, очевидно, будет равно 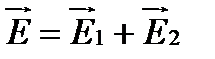и, следовательно:

,

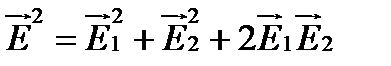т.е. общая интенсивность поля

,
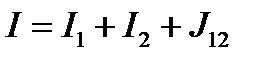где 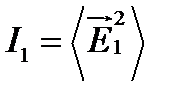; ; 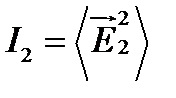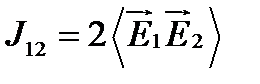– интерференционный член, показывающий отступление от принципа суперпозиции для интенсивностей волн. (При 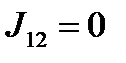интерференция отсутствует.)

Пусть 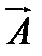и 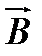− комплексные амплитуды волн, так что

, , , ,

, , , ,
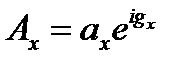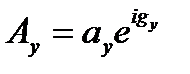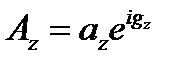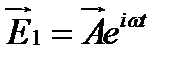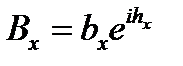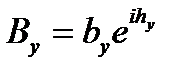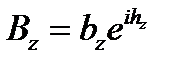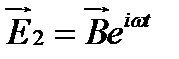где 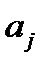и 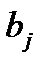– действительные амплитуды, ;

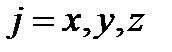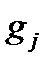и 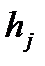– фазы, вообще говоря, различные, т.к. волны приходят в точку наблюдения P различными путями: ; ,

,

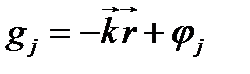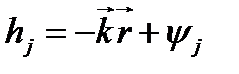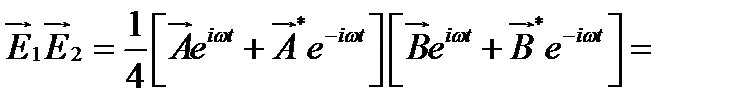
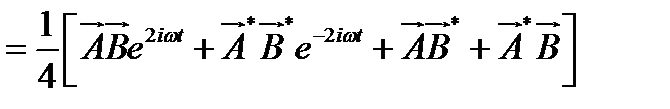следовательно, интерференционный член

,

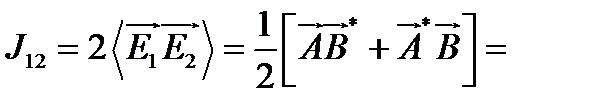
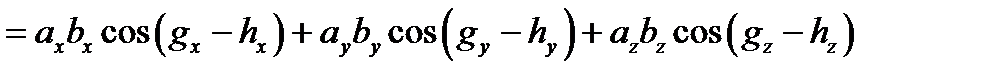На практике чаще всего осуществляется случай, когда между соответствующими компонентами возникает одна и та же разность фаз, т.е.

,

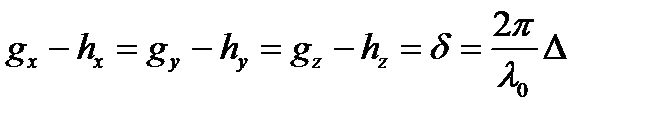где 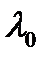– длина волны света в вакууме, ∆ – оптическая разность хода двух волн от общего источника до точки P. В этом случае

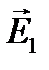
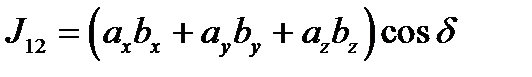, (8.2)

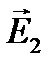
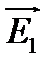Выражение (8.2) показывает, что интерференционный член зависит от амплитуды колебаний и разности фаз двух волн, приходящих в точку P. Рассмотрим частный случай, когда обе волны распространяются в одном направлении вдоль оси z и поляризованы в двух ортогональных плоскостях − в x0z и 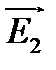в y0z (рис. 8.1).

Рис. 8.1 К доказательству поперечности световых волн

Тогда очевидно 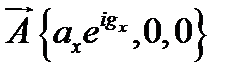, 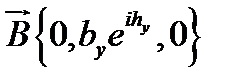и, следовательно 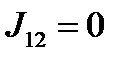– интерференция отсутствует. В истории развития оптики этот факт послужил доказательством поперечности световых волн. В 1816 году Френель и Араго обнаружили, что лучи, поляризованные во взаимно перпендикулярных плоскостях, не интерферируют, и Юнг в 1817 году на основе этого показал, что световые колебания поперечны. Действительно, пусть 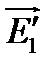и 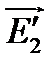не поперечные волны, тогда 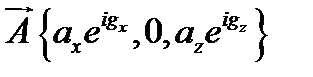, , 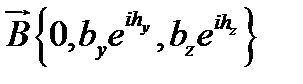следовательно, 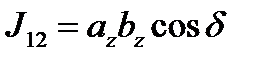и, поскольку 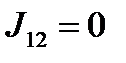, то следует заключить, что 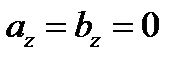, т.е. волны поперечны (электрические векторы обеих волн перпендикулярны оси z).

Пусть теперь обе волны поляризованы в одной плоскости, т.е.
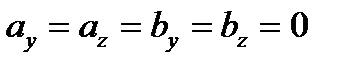, тогда ; ; .

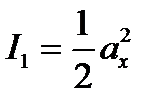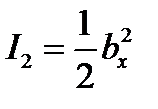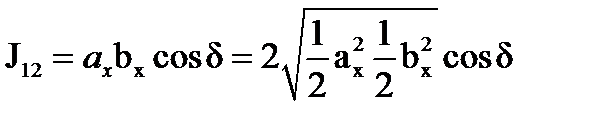Полная интенсивность имеет вид:

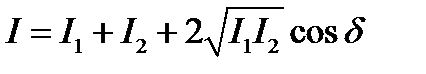. (8.3)

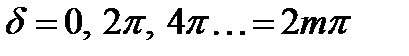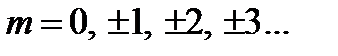Максимумы интенсивности имеют место при , где и равны:

.

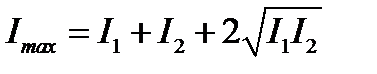Минимумы интенсивности будут в точках 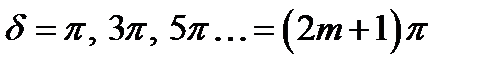, где
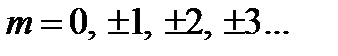и равны

.

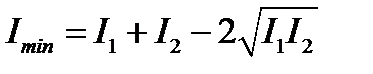При 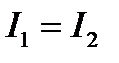получаем:

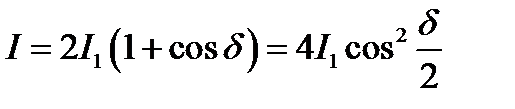. (8.4)

Не вдаваясь в строгое доказательство, отметим, что эти результаты справедливы и для случая неполяризованного света, поскольку пучок естественного света можно рассматривать как суперпозицию двух некогерентных пучков, линейно поляризованных под прямым углом друг к другу.