По виду допустимого множества

· Безусловная оптимизация, если 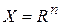. Отсутствуют ограничения и связи.

· Условная оптимизация, если 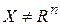. Присутствуют ограничения и/или связи.

По виду критерия оптимальности:

· Задачи математического программирования (критерий – функция);

· Вариационные задачи (критерий – функционал).

По критерию размерности допустимого множества:

· методы одномерной оптимизации;

· методы многомерной оптимизации.

По виду целевой функции и допустимого множества:

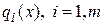· Задачи оптимизации, в которых целевая функция и ограничения являются линейными функциями, разрешаются так называемыми методами линейного программирования.

· В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

o если и 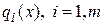— выпуклые функции, то такую задачу называют задачей выпуклого программирования;

o если 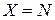, то имеют дело с задачей целочисленного (дискретного) программирования.

По объему необходимой информации для реализации метода, а также требованиям к гладкости и наличию у целевой функции частных производных:

· прямые методы, требующие только вычислений целевой функции в точках приближений (методы нулевого порядка);

· методы первого порядка: требуют вычисления первых частных производных функции;

· методы второго порядка: требуют вычисления вторых частных производных.

По способам анализа (технологии расчетов):

· аналитические методы (например, метод множителей Лагранжа);

· численные методы;

· графические методы.