Свойства функции одной переменной

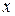Функция представляет собой правило, которое каждому значению ставит в соответствие единственное значение 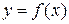. Пусть 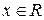, где 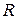- множество всех вещественных чисел. Пусть, кроме того задано множество 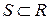. Если 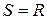говорят, что функция всюду определена. Если 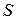есть собственное подмножество 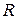, то функция определена в ограниченной области. Например,

,

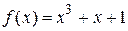где 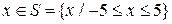, определена в ограниченной области.

Функция , определенная на множестве 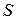, достигает своего глобального (абсолютного) минимума в точке 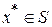в том и только том случае, если 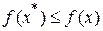для всех .

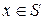Функция , определенная на множестве 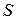, имеет локальный (относительный) минимум в точке 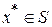в том и только том случае, если 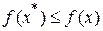для всех 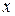удаленных от 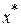на расстояние, меньшее 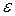, т.е. существует 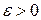, такое, что для всех 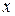, удовлетворяющих условию 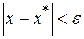, выполняется условие .

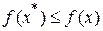Физические процессы могут описываться непрерывными функциями, т.е. функциями обладающими свойством непрерывности в каждой точке их определения. Однако в инженерной практике часто приходится использовать разрывные функции. Вполне возможны также случаи, когда переменная принимает только дискретные значения.

На рис. 2.1а представлен график функции, которая измеряет затраты на сообщение некоторой системе единицы количества тепла при различных температурах системы [6]. Затраты описываются разрывной функцией температуры системы; однако сама температура может принимать все значения в диапазоне от 200 до 3000 градусов.

График на рис. 2.1б, представляющий зависимость стоимости погонного мера трубы от ее диаметра, имеет вид последовательности точек, поскольку набор установленных размеров выпускаемых промышленностью труб дискретен и конечен.

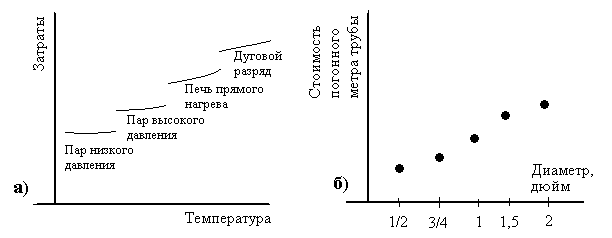
Рис. 2.1. Возможные графические представления функции одной переменной

В зависимости от того, является функция непрерывной или разрывной, а также в зависимости от структуры допустимой области, для отыскания точек оптимума могут использоваться различные методы. Метод эффективный при анализе непрерывных функций может оказаться неприменимым или неэффективным для разрывных функций.

Выпуклые функции.Задача оптимизации существенно усложняется, если функция может иметь в допустимой области несколько минимумов или максимумов. Поэтому значительный интерес представляют такие задачи, в которых целевая функция имеет только один экстремум и, соответственно, относительный экстремум является одновременно и абсолютным. Такие задачи связаны с понятиями выпуклости (вогнутости) функции.

Пусть – некоторая функция, заданная на выпуклом множестве 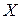; 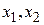- две произвольные точки из 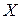. Функцию называют выпуклой, если она целиком лежит ниже (не выше) отрезка, соединяющего две ее произвольные точки, т.е. если при любых 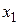и 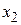, и при любом 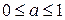значения функции в точке 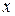будут не больше значений 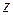отрезка, соединяющего 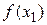и :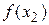

.

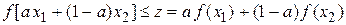Примеры выпуклых функций приведены на рисунке 2.2.

Рис. 2.2. Примеры выпуклых функций

Теорема. Сумма выпуклых функций есть выпуклая функция.

Рассмотрим некоторые важные виды выпуклых функций.

1. Линейная функция 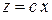является выпуклой на всем пространстве .

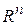2. Положительно (не отрицательно) определенная квадратичная форма 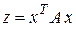является выпуклой функцией на всем пространстве .

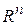3. Соответственно, сумма линейной функции и квадратичной формы выпукла, если квадратичная форма положительно определена.

Приведем без доказательства некоторые свойства выпуклых функций. Пусть выпуклая функция, заданная на выпуклом множестве 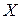. Тогда:

· Любой относительный минимум на 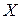является абсолютным;

· Не может быть двух и более относительных минимумов;

· Глобальный максимум достигается в одной или более крайних точках множества .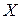

Монотонные функции. Функция является монотонной, если для двух произвольных точек 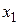и 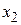, таких, что 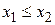, выполняется одно из следующих неравенств:

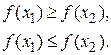
В первом случае функция монотонно убывает, в другом монотонно возрастает. При этом монотонная функция совсем не обязательно должна быть непрерывной.

Унимодальные функции. Функция является унимодальной на отрезке 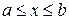в том случае, если она монотонна по обе стороны от единственной на рассматриваемом интервале оптимальной точки (точки экстремума) (рис.2.3)

Если функция унимодальна, то локальный минимум является и глобальным.

Если функция не унимодальна, то возможно наличие нескольких локальных минимумов, из которых путем перебора можно выбрать глобальный минимум.

Определения локального и глобального максимума можно получить, изменив знаки на противоположные.

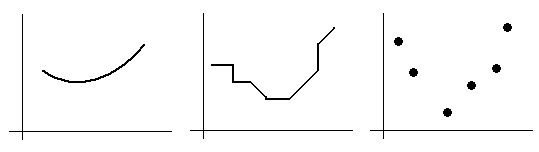
Рис. 2.3. Примеры унимодальных функций