Идентификация экстремумов функции одной переменной

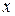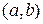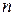Предположим, что функция одной переменной определена на открытом интервале и -кратно дифференцируема на этом интервале. Если 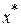внутренняя точка интервала, то теорема Тейлора позволяет записать изменения функции 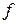при переходе от точки 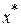к точке 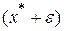в виде

.

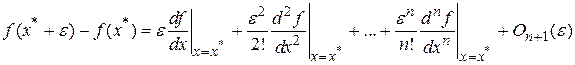Если 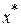локальный минимум функции 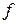, то по определению должна существовать 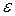-окрестность точки 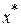, такая, что для всех 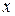из этой окрестности выполняется неравенство 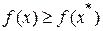. Отсюда следует, что

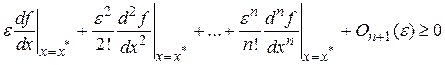. (2.1)

При достаточно малом 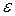можно считать первый член доминирующим. Поскольку 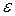может быть как положительным, так и отрицательным, то условие выполняется только при

.

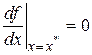В свою очередь, неравенство (2.1) будет справедливо только если

.

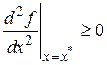Таким образом, необходимыми условиями того что точка 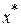является точкой локального минимума дважды дифференцируемой функции на открытом интервале 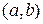являются следующие соотношения:

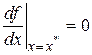, (2.2)

.

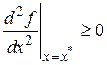Точка, отвечающая условию (2.2), называется стационарной точкой функции .

Эти условия являются необходимыми, но в общем случае недостаточными для существования экстремума, так как стационарная точка может быть точкой перегиба (седловой точкой).

Для того, чтобы определить является ли стационарная точка точкой максимума, минимума или точкой перегиба, можно воспользоваться следующей теоремой.

Теорема.Пусть в точке 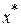первые 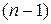производные функции обращаются в нуль, а производная порядка 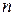отлична от нуля. Тогда:

· если 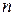нечетное, то 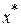точка перегиба;

· если 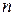четное, то 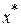точка локального экстремума;

· если эта производная положительна – то 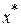точка минимума;

· если эта производная отрицательна – то 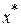точка максимума.

Для доказательства снова воспользуемся разложением отклонения в ряд Тейлора:

.

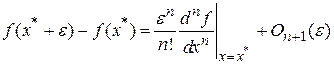Если 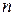нечетно, то правая часть может быть как положительной, так и отрицательной. Следовательно, функция не достигает в точке 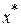экстремума, а является точкой перегиба. Если 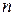четно, то 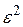всегда больше нуля. Тогда, если

,

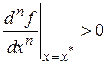то

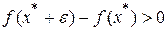
и имеет место минимум.

Пример.Пусть 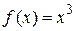. Стационарная точка это 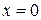. Вычислим

.

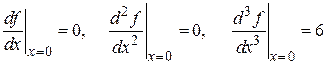Отсюда видно, что точка 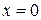есть точка перегиба.

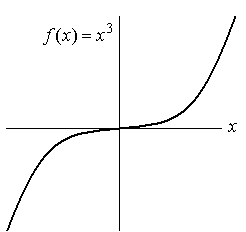
Рис. 2.4. Точка перегиба

Пример.Дана функция

,

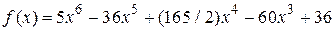определенная на всей вещественной оси. Первая производная данной функции равна

.

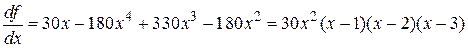Имеем четыре стационарные точки 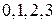. Вычислим вторую производную

.

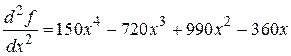Результаты сведены в таблицу 2.1.

Таблица 2.1

Стационарные точки по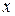
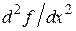
	27,5
		-120
	5,5

Для точек 1,2,3 вторая производная не равна нулю, следовательно, это точки экстремумов. При этом, точки 1 и 3 – точки минимумов, а 2 – точка максимума. Осталось проверить точку 0.

Возьмем третью производную

.

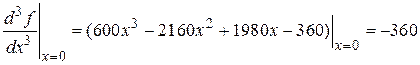Так как производная не равна нулю и имеет нечетный порядок, то 0 – точка перегиба.