Стягивание контура нефтеносности к эксплуатационной кольцевой батарее

Имеется кольцевая батарея из n (n>2) эксплуатацион­ных скважин, размещенных равномерно по окружности радиусом а. Контур питания удален от всех скважин на расстояние r_к, значительно превышающее а. Первоначально контур нефтеносности представляет собой окружность, концентричную по отношению к окружности – батарее и имеющую радиус r_н, причем r_нв несколько раз меньше r_к, но больше радиуса батареи а.

Подсчет времени движения частиц контура нефтеносности по линиям тока проведем по формуле (7.78). При этом характеристическую функцию течения определяем по формуле (7.71):

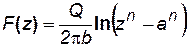, (7.79)

где Q – объемный дебит одной из скважин.

Таким образом

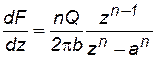. (7.80)

Величины z и `z запишем в полярной системе координат:

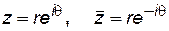. (7.81)

Тогда из (7.80) и (7.81) следует, что

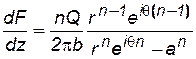. (7.82)

Рассматриваем движение частиц только вдоль прямых линий тока – главной и нейтральной (рис. 7.9). По всем главным линиям тока частицы контура нефтеносности движутся с одинаковой скоростью, по всем нейтральным линиям тока характер движения этих частиц также один и тот же. Поэтому достаточно найти время продвижения двух частиц контура: одной, которая движется по любой из главных линий тока, и другой, движущейся по любой из нейтральных линий.

Направим полярную ось из центра батареи вдоль одной из главных линий тока и будем искать время движения частицы контура нефтеносности вдоль полярной оси и по вдоль нейтральной линии, ближайщей к этой оси.

Так как для главных и нейтральных линий тока q=const, можно на основании второй формулы (7.81) определить dz следующим образом:

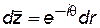. (7.83)

Подставляя значения dF/dz из (7.82) и dz из (7.83) в формулу (7.78), получим:

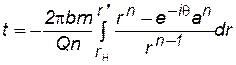, (7.84)

где r^/ – полярный радиус частицы.

Уравнение полярной оси имеет вид q=0. Подставляя это значение q в уравнение (7.84), получим формулу для вычисления времени движения частицы контура нефтеносности по главной линии тока:

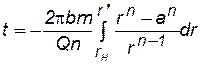, (7.85)

Уравнение нейтральной линии тока q=p/n.Подставим это значение q в (7.78) и заметим, что 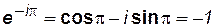. Тогда уравнение движения частицы кон­тура нефтеносности по нейтральной линии тока представится в виде

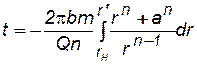. (7.86)

Из частиц контура нефтеносности раньше всех других достигнут скважин те, которые движутся по главным линиям тока, так как их пути – наикратчайшие. Когда частица контура, движущаяся по главной линии тока, подойдет к скважине, последняя начнет обводняться. В этот момент времени t_n,в уравнении (7.85) надо считать, что 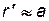. После интегрирования правой части (7.64), получим

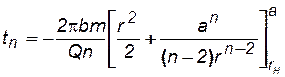. (7.87)

Определим точку нейтральной линии тока, в которой будет находиться частица контура нефтеносности в момент начала обводнения скважин t_n для этого раскроем интеграл правой части (7.86) и напишем это равенство для момента t_n:

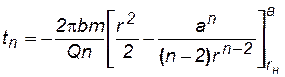. (7.88)

Местоположение частицы контура нефтеносности на нейтральной линии тока в момент прорыва воды в скважины можно определить, приравняв правые части формул (7.87) и (7.88) и решив затем полученное уравнение n-степени относительно r'.

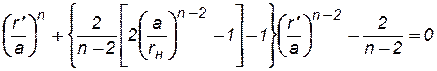. (7.89)

Исследуя уравнение (7.89), В. Н. Щелкачев установил, что величина r'/а возрастает с увеличением отношения r_н/a; следовательно, чем больше величина радиуса первоначального контура нефтеносности, тем больше отставание точек контура нефтеносности, движущихся по нейтральной линии тока, от точек контура, движущихся по главной линии тока..

При величине радиуса контура нефтеносности r_н более, чем в два раза превышающей радиус батареи а можно пренебрегать тем членом уравнения (7.89), который содержит множитель а/r_н. Тогда уравнение (7.89) принимает более простой вид

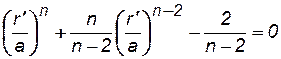. (7.90)

При n= 3 уравнение (7.90) сводится к кубическому уравнению, у которого левая часть раскладывается на множители. К кубическому уравнению сводится (7.90) и при n = 6. Если n = 4, получим биквадратное уравнение, если n=8 – уравнение четвертой степени.

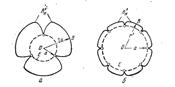
Рис.7.25. Контур нефтеносности в момент прорыва воды в скважины кольцевой батареи

На рис. 7.25 контуры нефтеносности вычерчены для трех и восьми скважин в момент прорыва в них воды. Чем больше скважин в батарее, тем меньше отставание частиц контура нефтеносности от тех, которые движутся по главной линии тока, т. е. тем равномернее стягивается контур.

Исследования при помощи формул (7.85) и (7.86) позволяют утверждать, что формы контура нефтеносности, которая первоначально была в виде окружности, искажается лишь в ближайшей окрестности скважин. При анализе явления стягивания контура к скважинам кольцевой батареи допустимо применить «галереизацию», т. е. кольцевую батарею заменить равнодебитной кольцевой галереей

Время безводной эксплуатации батареи t_n определяется формулой (7.87). Из этой же формулы легко определить: 1) общий объем добытой нефти за время безводной эксплуатации, 2) объем оставшейся в пласте нефти к начальному моменту обводнения скважин и 3) площадь, занятую оставшейся в пласте нефтью.

Действительно, общий объем добытой жидкости за время безвод­ной эксплуатации скважин Qnt_n подсчитывается по формуле (7.87) следующим образом:

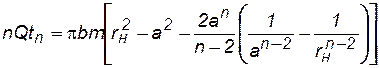. (7.91)

Объем оставшейся в пласте нефти определится по формуле

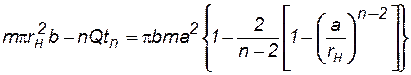. (7.92)

Наконец, площадь ω_н, занятая оставшейся в пласте нефтью в момент прорыва воды в скважины, находим по формуле

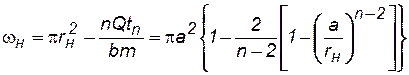. (7.93)

Если сравнить площадь оставшейся в пласте нефти ω_н с площадью круга, ограниченного кольцевой батареей скважин pа², получим значения отношения ω_н/pа², приведенные в таблице для а = 0,4r_ни0,1r_н.

Из таблицы видно, что при большом числе скважин в батарее нефтеносная площадь ω_н не зависит от величины отношения а/r_н.